Zadanie nr 9499969
Punkt 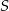 jest środkiem okręgu wpisanego w trapez
jest środkiem okręgu wpisanego w trapez 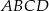 (
(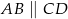 ). Wykaż, że trójkąt
). Wykaż, że trójkąt 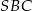 jest prostokątny.
jest prostokątny.
Rozwiązanie
Naszkicujmy sobie opisaną sytuację.
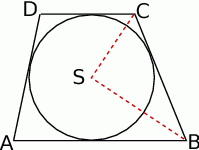
Ponieważ 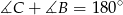 oraz odcinki
oraz odcinki 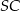 i
i 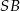 zawierają się w dwusiecznych kątów
zawierają się w dwusiecznych kątów 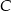 i
i 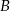 , mamy
, mamy
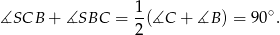
Zatem 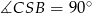 .
.

