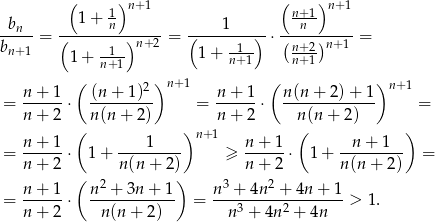Zadanie nr 5895658
Wykaż, że ciąg 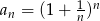 jest zbieżny.
jest zbieżny.
Rozwiązanie
Sposób I
Zaczniemy od lematu
Lemat
Dla dowolnego 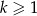 i
i 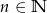 prawdziwa jest nierówność
prawdziwa jest nierówność
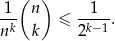
Dowód Liczymy
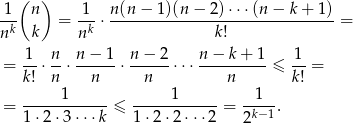
Korzystając z powyższego lematu, łatwo wykazać, że ciąg  jest ograniczony z góry. Korzystając z dwumianu Newtona i ze wzoru na sumę szeregu geometrycznego, mamy
jest ograniczony z góry. Korzystając z dwumianu Newtona i ze wzoru na sumę szeregu geometrycznego, mamy
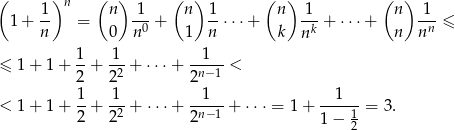
Pokażemy teraz, że ciąg 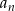 jest rosnącym, co zakończy dowód jego zbieżności. Aby pokazać monotoniczność wykorzystamy nierówność Bernoullego
jest rosnącym, co zakończy dowód jego zbieżności. Aby pokazać monotoniczność wykorzystamy nierówność Bernoullego
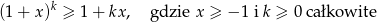
Mamy zatem
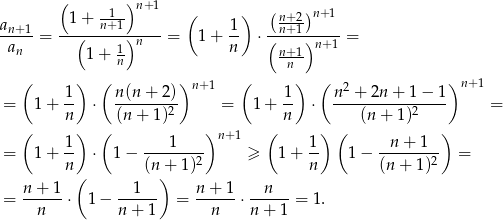
Zatem ciąg jest niemalejący. Gdyby uważnie przyjrzeć się nierówności Bernoullego, to byłoby jasne, że tak naprawdę powyższa nierówność jest ostra, czyli ciąg jest rosnący. Do dowodu wystarcza jednak słaba nierówność, więc nie będziemy się nad tym rozwodzić.
Sposób II
Rozważmy ciąg 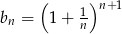 . Mamy
. Mamy
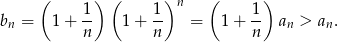
Podobnie jak poprzednio pokazujemy, że ciąg 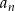 jest niemalejący. Pokażemy również, że ciąg
jest niemalejący. Pokażemy również, że ciąg 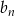 jest malejący, co na mocy powyższej nierówności oznacza, że
jest malejący, co na mocy powyższej nierówności oznacza, że
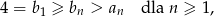
czyli ciąg 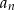 jest niemalejący i ograniczony z góry, a więc zbieżny.
jest niemalejący i ograniczony z góry, a więc zbieżny.
Wykażmy zatem, że ciąg 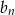 jest malejący. Jak poprzednio, będziemy korzystać z nierówności Bernoullego.
jest malejący. Jak poprzednio, będziemy korzystać z nierówności Bernoullego.