/Studia/Analiza/Ciągi/Granice/Na dowodzenie

Zadanie nr 9639148

Wykaż, że granica 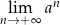n nl→im+∞ a

  • jest równa 0 dla |a| < 1 ;
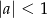  • jest równa 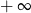+ ∞ dla a > 1 ;
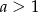  • nie istnieje dla a ≤ − 1 .
Wersja PDF

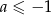Rozwiązanie

  • Ustalmy 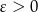𝜀 > 0 . Musimy pokazać, że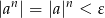
    |an| = |a|n < 𝜀

    dla prawie wszystkich n . Przekształcamy

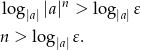
    log |a||a|n > lo g|a|𝜀 n > log |a|𝜀.

    Widać, że nierówność ta jest spełniona dla prawie wszystkich n .

  • Musimy pokazać, że dla dowolnego 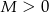M > 0 i dla prawie wszystkich n ,
    an > M .

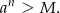
    Przekształcamy tę nierówność.

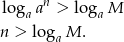
    n loga a > loga M n > loga M .

    Widać, że nierówność ta jest spełniona dla prawie wszystkich n .

  • Musimy wskazać dwa podciągi, które mają różne granice. Na mocy poprzedniego podpunktu mamy
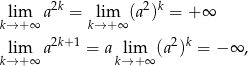
    lim a2k = lim (a2)k = + ∞ k→ + ∞ k→ + ∞ lim a2k+ 1 = a lim (a2)k = − ∞ , k→ + ∞ k→ +∞

    co dowodzi, że ciąg nie może być zbieżny.

Wersja PDF