/Studia/Analiza/Ciągi/Granice/Rekurencyjne

Zadanie nr 4102053

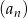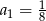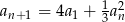Wykaż, że ciąg (an) jest zbieżny i oblicz jego granicę jeżeli 1 a1 = 8 i an+ 1 = 4a1 + 13a2n dla n ≥ 1 .

Wersja PDF

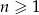Rozwiązanie

Wystarczy pokazać, że ciąg jest rosnący i ograniczony z góry. Zanim to jednak zrobimy policzmy jaką będzie ona miał granicę - to pomoże nam w dalszych rachunkach. Przechodzimy do granicy w równości 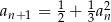a = 1 + 1a2 n+ 1 2 3 n :

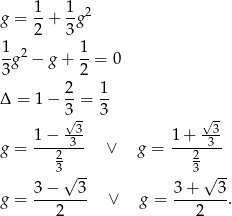
1- 1- 2 g = 2 + 3 g 1 1 --g2 − g+ --= 0 3 2 Δ = 1− 2-= 1- 3 3 √3- √3- g = 1−---3- ∨ g = 1+--3-- 23 23 √ -- √ -- g = 3−----3- ∨ g = 3+----3. 2 2

Pokażemy, że ciąg jest ograniczony z góry przez pierwszą z tych liczb, więc to będzie jego granica. Jest jasne, że 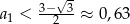√- a < 3−--3 ≈ 0 ,63 1 2 . Załóżmy, że 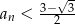√- a < 3−--3 n 2 . Wtedy

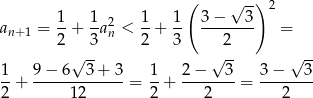
( √ -) 2 1- 1-2 1- 1- 3-−---3- an +1 = 2 + 3an < 2 + 3 2 = √ -- √ -- √ -- 1- 9-−-6--3-+-3- 1- 2-−---3- 3-−---3- 2 + 12 = 2 + 2 = 2

Zatem rzeczywiście ciąg jest ograniczony z góry przez 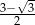3−√ 3 --2-- . Pozostało pokazać, że jest rosnący.

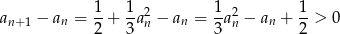
a − a = 1+ 1a2 − a = 1a2 − a + 1-> 0 n+1 n 2 3 n n 3 n n 2

Nierówność ta wynika z tego, że na lewo od pierwiastka 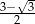3−√ 3 --2-- parabola 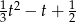1 t2 − t+ 1 3 2 jest powyżej osi Ox .  
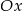Odpowiedź: 3− √3 --2--

Wersja PDF