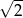Zadanie nr 2214269
Oblicz granicę 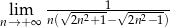 .
.
Rozwiązanie
Korzystamy ze wzoru 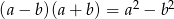 , żeby pozbyć się wyrażenia postaci
, żeby pozbyć się wyrażenia postaci  . Będziemy ponadto korzystać z tego, że
. Będziemy ponadto korzystać z tego, że 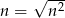 (będziemy wciągać
(będziemy wciągać  pod pierwiastek).
pod pierwiastek).
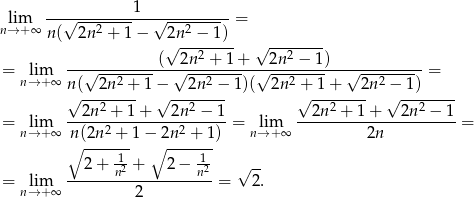
Odpowiedź: 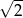
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 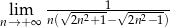 .
.
Korzystamy ze wzoru 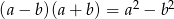 , żeby pozbyć się wyrażenia postaci
, żeby pozbyć się wyrażenia postaci  . Będziemy ponadto korzystać z tego, że
. Będziemy ponadto korzystać z tego, że 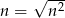 (będziemy wciągać
(będziemy wciągać  pod pierwiastek).
pod pierwiastek).
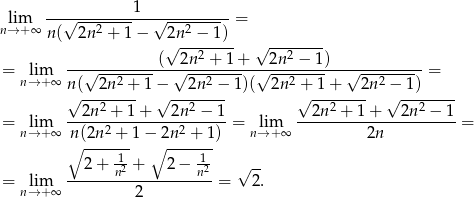
Odpowiedź: