Zadanie nr 2132558
Udowodnij, że jeżeli środki boków dwóch czworokątów wypukłych pokrywają się, to pola tych czworokątów są równe.
Rozwiązanie
Udowodnimy, że pole czworokąta powstałego przez połączenie środków jego boków jest równe połowie pola wyjściowego czworokąta. Fakt ten w szczególności oznacza, że środki boków jednoznacznie wyznaczają pole czworokąta, czyli to, co jest treścią naszego zadania.
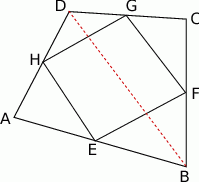
Niech 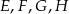 będą środkami boków czworokąta
będą środkami boków czworokąta 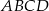 i poprowadźmy przekątną
i poprowadźmy przekątną 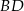 . Odcinki
. Odcinki 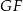 i
i 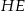 łączą środki boków w trójkątach
łączą środki boków w trójkątach 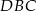 i
i 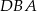 , zatem
, zatem
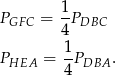
Dodając te równości stronami mamy
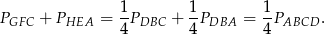
Podobnie pokazujemy, że
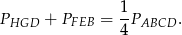
Mamy zatem


