/Konkursy/Zadania/Geometria/Planimetria/Czworokąt/Różne

Zadanie nr 6724459

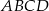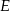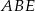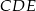Przekątne czworokąta wypukłego ABCD przecinają się w punkcie E . Wiadomo, że trójkąty ABE i CDE mają równe pola, długość boku 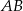AB jest równa 4, a przekątna 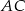AC jest zawarta w dwusiecznej kąta 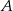A . Oblicz długość boku BC .

Wersja PDF

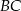Rozwiązanie

Oznaczmy odcinki na jakie dzieli przekątną punkt 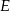E jak na rysunku.

PIC

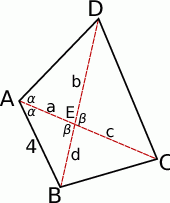
Warunek równości pól oznacza, że

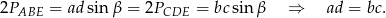
2PABE = ad sin β = 2PCDE = bcsin β ⇒ ad = bc.

Jeżeli zapiszemy ten warunek w postaci

a c --= -- b d

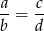
to widać, że oznacza on podobieństwo trójkątów 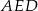AED i CEB (bo mają wspólny kąt między tymi bokami). W szczególności

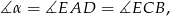
∡ α = ∡EAD = ∡ECB ,

czyli trójkąt 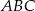ABC jest równoramienny. Stąd BC = 4 .  
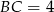Odpowiedź: BC = 4

Wersja PDF