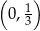/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Przechodzący przez punkty

Zadanie nr 2891411

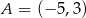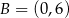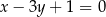Wyznacz środek okręgu przechodzącego przez punkty A = (− 5,3) i B = (0,6) , którego środek leży na prostej o równaniu x− 3y + 1 = 0 .

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

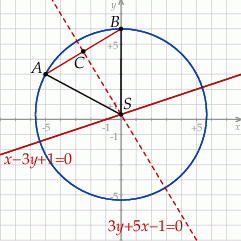
Szukany środek 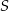S okręgu to punkt wspólny danej prostej, oraz symetralnej odcinka AB .

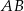Sposób I

Punkty 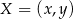X = (x,y) leżące na symetralnej odcinka 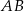AB to punkty, których odległości od końców tego odcinka są równe. Mamy zatem

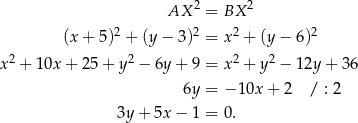
2 2 AX = BX 2 2 2 2 (x + 5) + (y − 3) = x + (y − 6) x 2 + 10x + 25+ y2 − 6y+ 9 = x2 + y2 − 12y + 3 6 6y = − 10x + 2 / : 2 3y + 5x− 1 = 0.

Symetralna odcinka 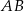AB ma więc równanie 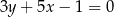3y+ 5x − 1 = 0 . Szukamy teraz jej punktu wspólnego z daną prostą.

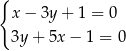
{ x− 3y + 1 = 0 3y + 5x − 1 = 0

Dodajemy równania stronami i mamy

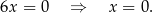
6x = 0 ⇒ x = 0.

Stąd 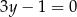3y − 1 = 0 , czyli 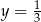1 y = 3 i ( 1) S = 0,3 .

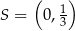Sposób II

Tym razem równanie symetralnej odcinka 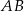AB napiszemy jako równanie prostej prostopadłej do 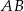AB i przechodzącej przez środek

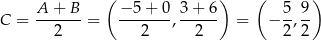
A + B ( − 5 + 0 3+ 6 ) ( 5 9 ) C = -------= -------, ------ = − -,-- 2 2 2 2 2

tego odcinka. Zauważmy najpierw, że współczynnik kierunkowy prostej 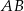AB jest równy

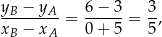
yB-−-yA- = 6−-3-= 3-, xB − xA 0+ 5 5

więc symetralna odcinka 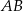AB musi mieć równanie postaci 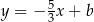y = − 53x + b . Współczynnik 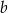b wyznaczamy podstawiając współrzędne punktu C .

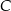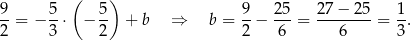
( ) 9-= − 5⋅ − 5- + b ⇒ b = 9-− 2-5 = 2-7−-2-5 = 1-. 2 3 2 2 6 6 3

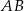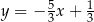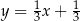Symetralna odcinka AB ma więc równanie y = − 5x + 1 3 3 . Szukamy teraz jej punktu wspólnego z podaną prostą: 1 1 y = 3x + 3 .

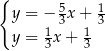
{ 5 1 y = − 3x+ 3 y = 13x + 13

Odejmujemy od pierwszego równania drugie i mamy

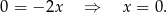
0 = − 2x ⇒ x = 0.

Stąd 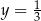y = 1 3 i ( ) S = 0 , 1 3 .

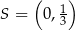Sposób III

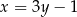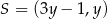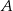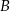Wiemy, że szukany środek okręgu leży on na prostej x = 3y − 1 , więc ma współrzędne postaci S = (3y − 1,y ) . Punkt ten musi być równo odległy od punktów A i B – zapiszmy ten warunek.

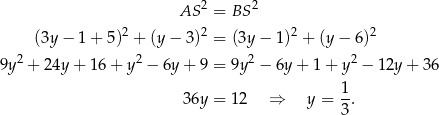
AS 2 = BS2 (3y − 1+ 5 )2 + (y − 3)2 = (3y− 1)2 + (y− 6)2 2 2 2 2 9y + 24y + 16 + y − 6y + 9 = 9y − 6y+ 1+ y − 12y + 36 1- 36y = 12 ⇒ y = 3.

Zatem środek okręgu ma współrzędne 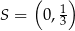( 1) S = 0,3 .  
Odpowiedź: ( ) 1 0,3

Wersja PDF