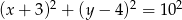Zadanie nr 5299193
Napisz równanie okręgu, którego środek znajduje się na prostej 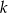 , przechodzącego przez punkty
, przechodzącego przez punkty 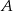 i
i 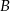 , jeśli
, jeśli 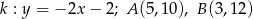 .
.
Rozwiązanie
Zaczynamy od rysunku.
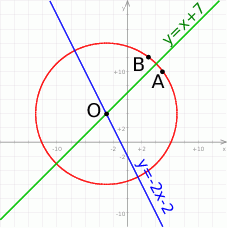
Napiszmy warunek, że punkty 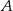 i
i 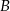 są równo odległe od pewnego punktu
są równo odległe od pewnego punktu 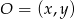 prostej
prostej 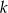 (ten punkt to oczywiście szukany środek okręgu).
(ten punkt to oczywiście szukany środek okręgu).
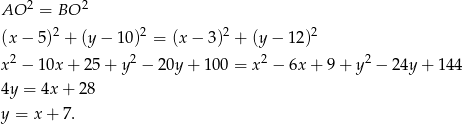
To co wyznaczyliśmy, to dokładnie symetralna odcinka 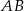 , oczywiście mogliśmy ją wyznaczyć na różne inne sposoby.
, oczywiście mogliśmy ją wyznaczyć na różne inne sposoby.
Korzystamy teraz z tego, że punkt 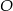 leży na prostej
leży na prostej 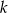 :
:
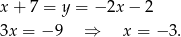
Zatem 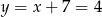 i
i 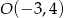 . Pozostało wyliczyć promień.
. Pozostało wyliczyć promień.
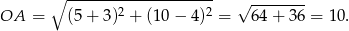
Zatem okrąg ma równanie
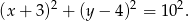
Odpowiedź: