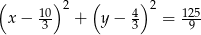/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Przechodzący przez punkty

Zadanie nr 9239887

Dodaj do ulubionych
Dodaj do rozwiązanych

Okrąg przechodzi przez punkty 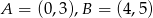A = (0,3),B = (4,5) , a jego środek należy do prostej o równaniu 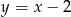y = x − 2 . Wyznacz równanie tego okręgu.

Rozwiązanie

Środek okręgu leży na prostej 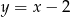y = x − 2 , więc jest postaci

S = (x,x − 2 ).

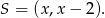
Okrąg przechodzi przez punkty 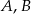A ,B , więc muszą one być w takiej samej odległości od punktu S .

PIC

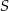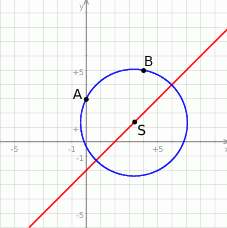
Liczymy

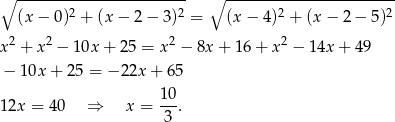
∘ ----------------------- ∘ ----------------------- (x − 0 )2 + (x − 2 − 3)2 = (x − 4)2 + (x− 2− 5)2 x2 + x2 − 10x + 2 5 = x2 − 8x + 16 + x2 − 14x + 49 − 10x + 25 = − 22x + 65 12x = 40 ⇒ x = 10. 3

Zatem środek ma współrzędne

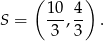
( ) S = 10-, 4 . 3 3

Teraz pozostało tylko obliczyć promień. Policzymy odległość punktu 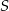S od punktu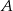 A

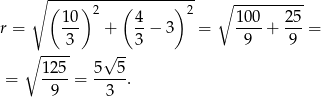
∘ -------------------- ( ) 2 ( )2 ∘ ---------- r = 1-0 + 4-− 3 = 100-+ 25-= 3 3 9 9 ∘ ---- √ -- = 125-= 5--5. 9 3

Zatem okrąg ma równanie

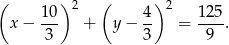
( )2 ( ) 2 x − 10- + y − 4- = 125. 3 3 9

 
Odpowiedź: ( ) ( ) x − 10 2 + y− 4 2 = 125 3 3 9

Wersja PDF