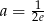Zadanie nr 2424396
Dla jakich wartości parametru  parabola
parabola 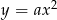 jest styczna do krzywej
jest styczna do krzywej 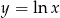 .
.
Rozwiązanie
Krzywe będą styczne, jeżeli funkcja 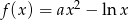 będzie miała miejsce zerowe, które jest jednocześnie miejscem zerowym pochodnej (czyli funkcje się przecinają w punkcie, w którym styczne do obu wykresów mają ten sam kierunek). Sprawdźmy jakie są miejsca zerowe pochodnej (bo łatwiej to zrobić niż sprawdzać miejsca zerowe
będzie miała miejsce zerowe, które jest jednocześnie miejscem zerowym pochodnej (czyli funkcje się przecinają w punkcie, w którym styczne do obu wykresów mają ten sam kierunek). Sprawdźmy jakie są miejsca zerowe pochodnej (bo łatwiej to zrobić niż sprawdzać miejsca zerowe 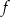 ).
).
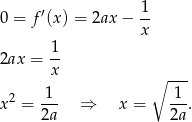
Pozostało sprawdzić kiedy jest to miejsce zerowe funkcji 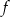 .
.
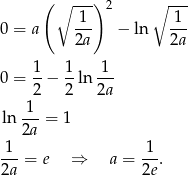
Na koniec, dla ciekawskich, wykresy obu funkcji.
Odpowiedź: