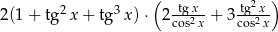Zadanie nr 2596758
Oblicz pochodną funkcji 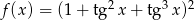 .
.
Rozwiązanie
Korzystamy ze wzoru na pochodną złożenia
![′ ′ ′ [f(g(x))] = f (g(x)) ⋅g (x)](https://img.zadania.info/zad/2596758/HzadR0x.gif)
oraz ze wzoru
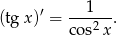
Liczymy
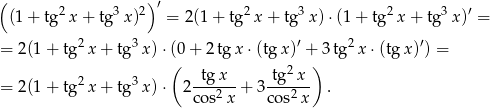
Odpowiedź: 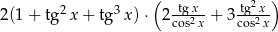
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz pochodną funkcji 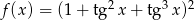 .
.
Korzystamy ze wzoru na pochodną złożenia
![′ ′ ′ [f(g(x))] = f (g(x)) ⋅g (x)](https://img.zadania.info/zad/2596758/HzadR0x.gif)
oraz ze wzoru
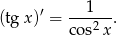
Liczymy
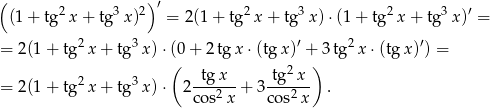
Odpowiedź: