/Studia/Analiza/Funkcje

Zadanie nr 2828409

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę funkcji ∘ --------x2−2- a rcco s(2x−1) .

Rozwiązanie

Oczywiście wyrażenie pod pierwiastkiem musi być nieujemne – to jednak jest spełnione zawsze, bo zbiorem wartości funkcji 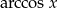arccosx jest przedział [0,π ] .

Mianownik musi być różny od zera, czyli 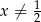x ⁄= 1 2 .

Pozostaje warunek z dziedziną 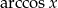arccos x ,

x2 − 2 x2 − 2 − 1 ≤ ------- ∧ -------≤ 1 2x − 1 2x− 1 x2-−-2-+-2x-−-1- x2 −-2−--2x+--1- 0 ≤ 2x − 1 ∧ 2x − 1 ≤ 0 2 2 0 ≤ x--+-2x-−-3- ∧ x-−--2x−--1-≤ 0 2x − 1 2x − 1 Δ = 4 + 12 = 16 ∧ Δ = 4 + 4 = 8 √ -- √ -- x 1 = − 3,x2 = 1 ∧ x 1 = 1− 2,x2 = 1 + 2 √ -- √ -- 0 ≤ (x-+-3)(x-−-1)- ∧ (x−--1+----2)(x−--1−----2)-≤ 0 [ 2x)− 1 2x− 1 ( ] 1 √ -- 1 √ -- x ∈ − 3,-- ∪ [1 ,+∞ ] ∧ x ∈ (−∞ ,1 − 2 ]∪ -,1 + 2 2 √ -- √ -- 2 x ∈ [− 3,1 − 2] ∪ [1 ,1+ 2].

 
Odpowiedź: √ -- √ -- x ∈ [− 3,1 − 2]∪ [1,1 + 2]

Wersja PDF