Zadanie nr 7108946
Uzasadnij, że nie istnieje granica 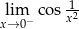 .
.
Rozwiązanie
Musimy pokazać dwa ciągi 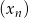 i
i 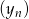 takie, że
takie, że
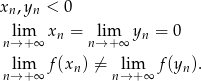
Łatwo takie ciągi wskazać: np. 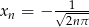 i
i 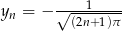 . Mamy
. Mamy
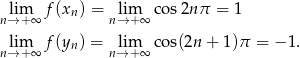
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że nie istnieje granica 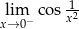 .
.
Musimy pokazać dwa ciągi 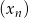 i
i 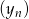 takie, że
takie, że
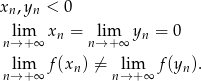
Łatwo takie ciągi wskazać: np. 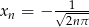 i
i 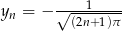 . Mamy
. Mamy