/Studia/Analiza/Funkcje/Klasy funkcji/Funkcje cyklometryczne/Uprość wyrażenie

Zadanie nr 8647464

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz wartość wyrażenia: 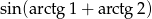sin(arctg 1+ arctg 2) .

Rozwiązanie

Żeby trochę uprościć sobie zapis oznaczmy

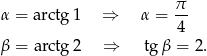
π α = arctg 1 ⇒ α = 4- β = a rctg 2 ⇒ tg β = 2 .

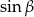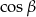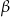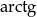Wyliczmy najpierw sin β i co sβ . W poniższym wyliczeniu ważne jest, że β jest kątem ostrym – to wynika z definicji funkcji a rctg .

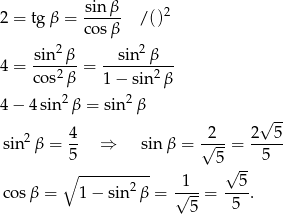
2 = tgβ = sin-β /()2 cos β 2 2 4 = sin--β = --sin--β--- cos2 β 1− sin 2β 2 2 4− 4 sin β = sin β √ -- 2 4 2 2 5 sin β = -- ⇒ sinβ = √---= ----- 5 5√ -- 5 ∘ -------2-- 1 5 cos β = 1 − sin β = √---= ----. 5 5

Liczymy teraz żądany sinus.

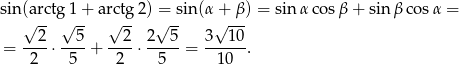
sin (arctg 1 + arctg2 ) = sin (α+ β) = sin αco sβ + sinβ cos α = √ -- √ -- √ -- √ -- √ --- --2- --5- ---2 2--5- 3--10- = 2 ⋅ 5 + 2 ⋅ 5 = 10 .

 
Odpowiedź: 3√-10 10

Wersja PDF