Zadanie nr 5824356
Oblicz pole elipsy 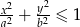 , gdzie
, gdzie 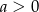 i
i 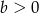 .
.
Rozwiązanie
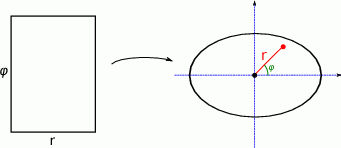
Na początek obrazek.
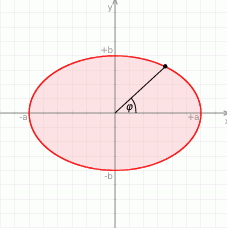
Sposób I
Pole elipsy 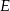 jest równe całce podwójnej
jest równe całce podwójnej
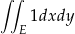
Całkę liczymy zmieniając współrzędne
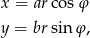
gdzie 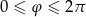 i
i 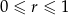 .
.
Liczymy jakobian tej zmiany zmiennych
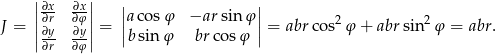
Mamy zatem
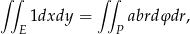
gdzie całkę z prawej strony liczymy po prostokącie 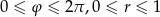 . Teraz całkę podwójną zamieniamy na całkę iterowaną.
. Teraz całkę podwójną zamieniamy na całkę iterowaną.
![( ) ( ) ∫ ∫ ∫ 1 ∫ 2π ∫ 1 ∫ 2π abrdφdr = ab rdφ dr = ab r 1d φ dr = P 0 0 [ 0 ] 0 ∫ 1 ∫ 1 1 2 1 = ab r ⋅2πdr = 2πab rdr = 2πab 2r = πab . 0 0 0](https://img.zadania.info/zad/5824356/HzadR10x.gif)
Sposób II
Rozwiązując nierówność opisującą elipsę względem zmiennej 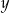 otrzymujemy układ dwóch nierówności:
otrzymujemy układ dwóch nierówności:
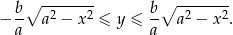
Ponadto  zmienia się w przedziale
zmienia się w przedziale ![[−a ,a]](https://img.zadania.info/zad/5824356/HzadR14x.gif) .
.
Stąd pole elipsy równa się
![∫ a [ b∘ -------- b ∘ -------] 2b ∫ a ∘ -------- P = -- a2 − x 2 +-- a2 − x2 dx = --- a2 − x2dx −a a a a −a](https://img.zadania.info/zad/5824356/HzadR15x.gif)
Ostatnią całkę obliczymy przez podstawienie
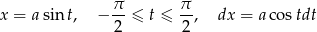
Liczymy
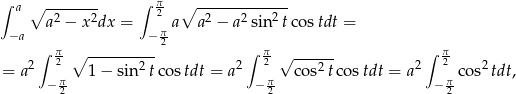
bo 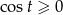 dla
dla ![π- π- t ∈ [− 2 ,2]](https://img.zadania.info/zad/5824356/HzadR19x.gif) . Aby obliczyć ostatnią całką korzystamy ze wzoru
. Aby obliczyć ostatnią całką korzystamy ze wzoru 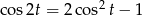 .
.
![∫ π2 ∫ π2 1 + co s2t [∫ π2 1 ∫ π2 cos2t ] a2 cos2tdt = a2 ----------dt = a2 -dt + ------dt = − π2 −π2 2 − π2 2 − π2 2 [ ]π2 2 = a2 t-+ sin2t- = a-π-. 2 4 − π2 2](https://img.zadania.info/zad/5824356/HzadR21x.gif)
Zatem pole elipsy równa się
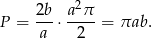
Sposób III
Tym razem skorzystamy z dwuwymiarowej wersji twierdzenia Stokesa, czyli z twierdzenia Greena
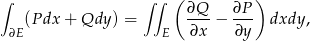
gdzie 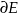 jest dodatnio zorientowanym brzegiem obszaru
jest dodatnio zorientowanym brzegiem obszaru 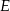 . Chcemy z prawej strony tego wzoru mieć
. Chcemy z prawej strony tego wzoru mieć 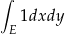 , więc bierzemy np.
, więc bierzemy np. 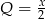 i
i 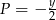 . i mamy
. i mamy
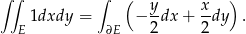
Całkę krzywoliniową z prawej strony liczymy parametryzując brzeg elipsy wzorem
![(x,y) = (a cosφ ,bsin φ), gdzie φ ∈ [0,2π ]](https://img.zadania.info/zad/5824356/HzadR30x.gif)
Mamy zatem
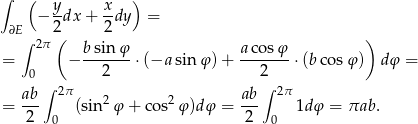
Sposób IV
Tym razem skorzystamy ze znanego wzoru na pole koła i odrobiny algebry liniowej.
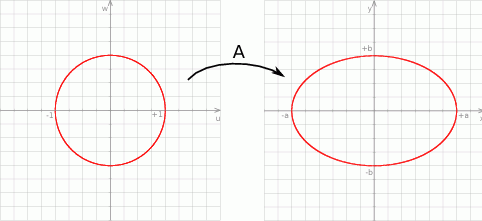
Jeżeli 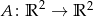 jest afinicznym odwzorowaniem liniowym
jest afinicznym odwzorowaniem liniowym
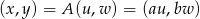
to odwzorowanie to zmienia pole powierzchni tak, jak jego wyznacznik, czyli mnoży pole powierzchni przez
![[ ] d etA = det a 0 = ab. 0 b](https://img.zadania.info/zad/5824356/HzadR35x.gif)
Ponadto, obrazem okręgu jednostkowego
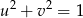
przy tym odwzorowaniu jest krzywa opisana równaniem
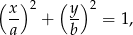
czyli dana elipsa. Zatem pole elipsy jest równe 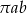 .
.
Odpowiedź: