Zadanie nr 4220739
- Wykaż, że równanie
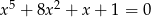 nie ma rozwiązań w przedziale
nie ma rozwiązań w przedziale 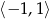 .
. - Wykaż, że równanie
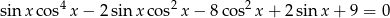
nie ma rozwiązań rzeczywistych.
Rozwiązanie
- Równanie wygląda na trudne do rozwiązania, bo nie ma pierwiastków wymiernych (dzielniki wyrazu wolnego nie są pierwiastkami). My jednak nie mamy tego równania rozwiązać, a jedynie pokazać, że nie ma ono rozwiązań w przedziale
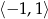 .
. Aby to zrobić, zapiszmy równanie w postaci
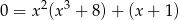
Zauważmy teraz, że
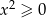 ,
, 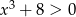 (bo
(bo 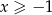 ) oraz
) oraz 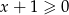 . Zatem oba składniki z prawej strony równania są nieujemne. Ponadto, pierwszy zeruje się tylko dla
. Zatem oba składniki z prawej strony równania są nieujemne. Ponadto, pierwszy zeruje się tylko dla 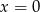 , a drugi tylko dla
, a drugi tylko dla 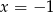 , co oznacza, że prawa strona równania jest zawsze dodatnia. To oznacza, że równanie jest sprzeczne.
, co oznacza, że prawa strona równania jest zawsze dodatnia. To oznacza, że równanie jest sprzeczne. - Zauważmy, że w podanym równaniu występują tylko parzyste potęgi
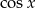 , więc przy pomocy jedynki trygonometrycznej możemy zamienić wszystkie cosinusy na sinusy.
, więc przy pomocy jedynki trygonometrycznej możemy zamienić wszystkie cosinusy na sinusy. 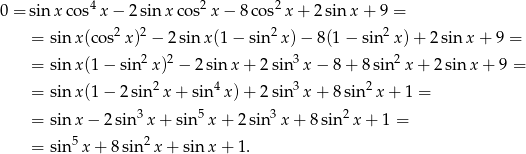
Możemy teraz podstawić
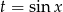 i otrzymujemy równanie wielomianowe z poprzedniego podpunktu.
i otrzymujemy równanie wielomianowe z poprzedniego podpunktu. 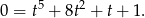
Ponieważ
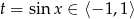 , z poprzedniego podpunktu wynika, że równanie to jest sprzeczne.
, z poprzedniego podpunktu wynika, że równanie to jest sprzeczne.

