/Szkoła podstawowa/Geometria/Czworokąty/Równoległobok

Zadanie nr 3699425

Dodaj do ulubionych
Dodaj do rozwiązanych

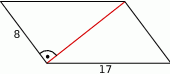
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.

PIC

Rozwiązanie

Dany równoległobok składa się z dwóch przystających trójkątów prostokątnych o jednej przyprostokątnej długości 8 i przeciwprostokątnej długości 17. Korzystając z twierdzenia Pitagorasa obliczamy długość drugiej przyprostokątnej tego trójkąta.

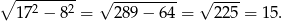
∘ --------- √ --------- √ ---- 172 − 82 = 289 − 6 4 = 225 = 15.

Obliczamy pole i obwód równoległoboku.

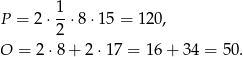
1- P = 2 ⋅2 ⋅8 ⋅15 = 120 , O = 2 ⋅8 + 2 ⋅17 = 16 + 34 = 50.

 
Odpowiedź: Pole: 120, obwód: 50.

Wersja PDF