/Szkoła podstawowa/Geometria/Czworokąty/Równoległobok

Zadanie nr 6623988

Dodaj do ulubionych
Dodaj do rozwiązanych

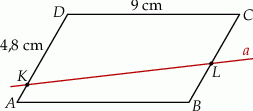
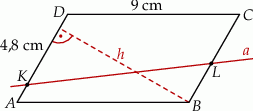
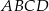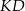Równoległobok ABCD o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej a na dwa trapezy tak, jak pokazano na rysunku. Odcinek KD ma długość 4,8 cm.

PIC

Pole trapezu 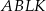ABLK jest trzykrotnie mniejsze od pola równoległoboku 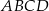ABCD . Oblicz długość odcinka 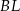BL . Zapisz obliczenia.

Rozwiązanie

Niech 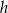h będzie wysokością równoległoboku opuszczoną na bok AD .

PIC

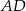W takim razie pole równoległoboku jest równe

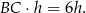
BC ⋅ h = 6h.

Pole trapezu 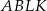ABLK jest trzy razy mniejsze, więc

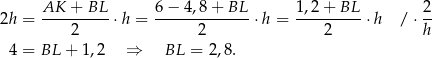
AK + BL 6 − 4 ,8+ BL 1,2+ BL 2 2h = ----------⋅h = ------------- ⋅h = ---------⋅ h / ⋅-- 2 2 2 h 4 = BL + 1 ,2 ⇒ BL = 2,8.

 
Odpowiedź: 2,8 cm

Wersja PDF