/Szkoła podstawowa/Geometria/Czworokąty/Równoległobok

Zadanie nr 6677089

Ada wycięła z kartonu równoległobok 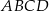ABCD o bokach 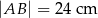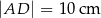|AB | = 24 cm , |AD | = 10 cm i polu równym 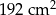192 cm 2 (rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej 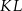KL i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.

PIC

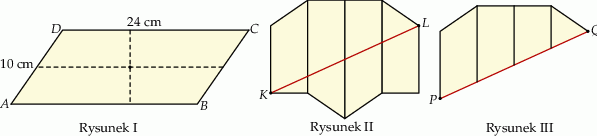
Oblicz obwód wielokąta z rysunku III.

Wersja PDF

Rozwiązanie

Podane pole równoległoboku pozwala nam obliczyć wysokość każdego z trapezów, na które został rozcięty.

PIC

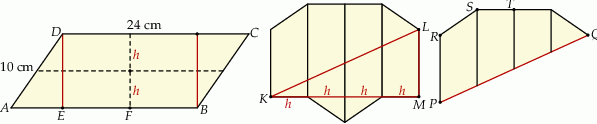
Jeżeli oznaczymy tę wysokość przez 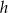h , to mamy

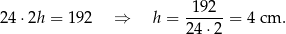
24 ⋅2h = 192 ⇒ h = -192--= 4 cm . 24 ⋅2

Z twierdzenia Pitagorasa w trójkącie 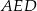AED mamy

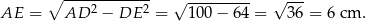
∘ ---2------2- √ --------- √ --- AE = AD − DE = 100 − 64 = 3 6 = 6 cm .

Możemy teraz obliczyć długość krótszej podstawy mniejszego z utworzonych trapezów

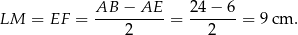
LM = EF = AB-−--AE--= 24−--6-= 9 cm . 2 2

To z kolei pozwala obliczyć długość odcinka 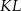KL . Piszemy twierdzenie Pitagorasa w trójkącie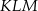 KLM

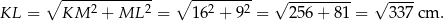
∘ ------------- ∘ --------- √ --------- √ ---- KL = KM 2 + ML 2 = 162 + 92 = 256 + 8 1 = 337 cm .

Obwód wielokąta z rysunku III jest więc równy

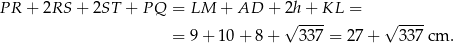
PR + 2RS + 2ST + P Q = LM + AD + 2h + KL = √ ---- √ ---- = 9+ 10 + 8+ 337 = 2 7+ 337 cm .

 
Odpowiedź: √ ---- 27 + 33 7 cm

Wersja PDF