Zadanie nr 9517971
Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.
Rozwiązanie
Zaczynamy od rysunku i oznaczmy 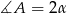 ,
, 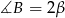 .
.
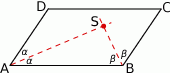
Ponieważ 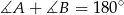 , mamy
, mamy
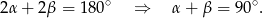
Zatem z trójkąta 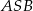 mamy
mamy
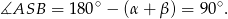
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.
Zaczynamy od rysunku i oznaczmy 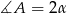 ,
, 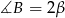 .
.

Ponieważ 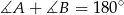 , mamy
, mamy
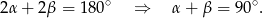
Zatem z trójkąta 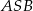 mamy
mamy