/Szkoła podstawowa/Geometria/Czworokąty/Równoległobok

Zadanie nr 9836945

Dodaj do ulubionych
Dodaj do rozwiązanych

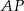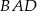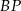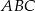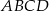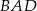Półprosta AP jest dwusieczną kąta BAD i półprosta BP jest dwusieczną kąta ABC w równoległoboku ABCD . Kąt BAD jest równy 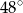48∘ . Oblicz miarę kąta 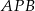AP B . Zapisz obliczenia.

PIC

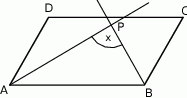
Rozwiązanie

Wiemy, że prosta 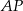AP jest dwusieczną kąta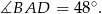 ∘ ∡BAD = 48 .

PIC

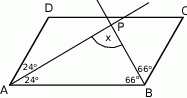
Zatem

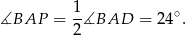
∡BAP = 1-∡BAD = 24∘. 2

Podobnie,

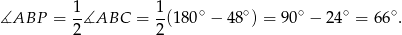
1 1 ∡ABP = --∡ABC = -(180 ∘ − 4 8∘) = 90∘ − 24∘ = 66∘. 2 2

Teraz wystarczy skorzystać z tego, że suma kątów w trójkącie 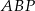ABP jest równa ∘ 18 0 .

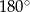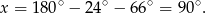
∘ ∘ ∘ ∘ x = 18 0 − 24 − 66 = 90 .

 
Odpowiedź: 90∘

Wersja PDF