/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Udowodnij

Zadanie nr 1388144

Dodaj do ulubionych
Dodaj do rozwiązanych

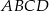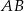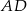Dany jest prostokąt ABCD . Okręgi o średnicach AB i AD przecinają się w punktach 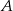A i P .

PIC

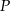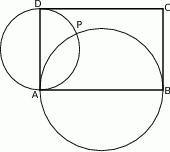
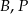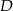Wykaż, że punkty B,P i D leżą na jednej prostej.

Rozwiązanie

Połączmy punkt 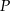P z punktami 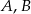A ,B i D .

PIC

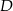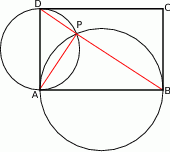
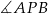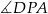Zauważmy, że oba kąty ∡AP B i ∡DPA są oparte na średnicach, czyli

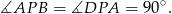
∡AP B = ∡DPA = 90∘.

To jednak oznacza, że

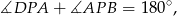
∡DPA + ∡AP B = 180∘,

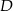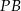czyli punkt D leży na prostej PB .

Wersja PDF