Zadanie nr 3170525

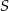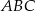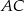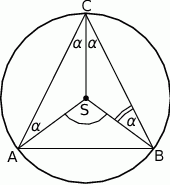
Środek okręgu opisanego na trójkącie równoramiennym ABC , o ramionach i 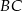, leży wewnątrz tego trójkąta (zobacz rysunek).

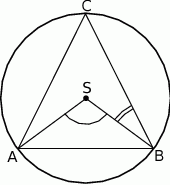
Wykaż, że miara kąta wypukłego 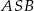ASB jest cztery razy większa od miary kąta wypukłego SBC .

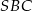Rozwiązanie

Oznaczmy 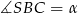∡SBC = α .

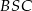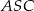Zauważmy teraz, że trójkąty BSC i ASC są równoramienne i przystające, więc

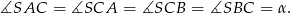
∡SAC = ∡SCA = ∡SCB = ∡SBC = α.

Stąd

∡ASB = 3 60∘− ∡ASC − ∡BSC = 360∘ − (180 ∘− 2α )− (1 80∘− 2α) = 4α .

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz