Zadanie nr 4225565
Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Uzasadnij, że środki tych okręgów są wierzchołkami czworokąta, w który można wpisać okrąg.
Rozwiązanie
Zróbmy rysunek.
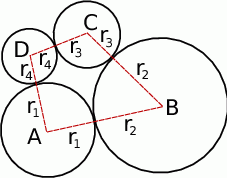
W zadaniu kluczowe jest to, że odległość środków okręgów stycznych zewnętrznie jest równa sumie ich promieni. Mamy zatem
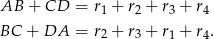
I koniec, bo równość sum przeciwległych boków to warunek wystarczający na to, aby w czworokąt można było wpisać okrąg.

