Zadanie nr 6013926
Okrąg dopisany do boku 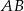 trójkąta
trójkąta 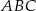 to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków
to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków 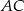 i
i 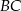 .
.
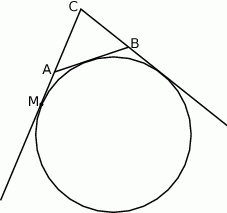
Wykaż, że jeżeli 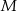 jest punktem styczności tego okręgu z przedłużeniem boku
jest punktem styczności tego okręgu z przedłużeniem boku 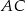 to długość odcinka
to długość odcinka 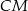 jest równa połowie obwodu trójkąta
jest równa połowie obwodu trójkąta 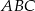 .
.
Rozwiązanie
Oznaczmy punkty styczności okręgu dopisanego z bokiem 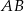 i przedłużeniem boku
i przedłużeniem boku 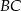 przez
przez 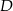 i
i 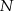 odpowiednio.
odpowiednio.
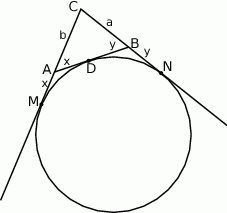
Przyjmijmy ponadto oznaczenia jak na rysunku, czyli 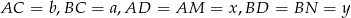 . Odcinki
. Odcinki 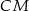 i
i 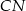 jako odcinki stycznych mają tę samą długość więc
jako odcinki stycznych mają tę samą długość więc
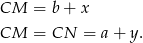
Dodając te dwie równości stronami mamy
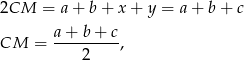
gdzie oznaczyliśmy 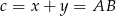 .
.

