Zadanie nr 7389711
Dany jest okrąg 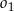 . Kreślimy cięciwę
. Kreślimy cięciwę 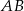 nieprzechodzącą przez środek okręgu
nieprzechodzącą przez środek okręgu 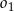 , a następnie rysujemy okrąg
, a następnie rysujemy okrąg 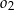 współśrodkowy z okręgiem
współśrodkowy z okręgiem 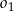 i styczny do cięciwy
i styczny do cięciwy 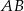 . Okręgi
. Okręgi 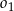 i
i 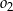 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu
ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu 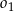 (zależy tylko od długości cięciwy
(zależy tylko od długości cięciwy 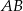 ).
).
Rozwiązanie
Zacznijmy od rysunku i oznaczmy promienie okręgów 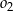 i
i 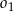 przez
przez  i
i 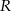 odpowiednio, oraz długość cięciwy przez
odpowiednio, oraz długość cięciwy przez 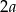 .
.
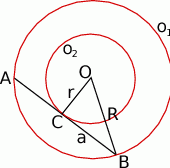
Pole pierścienia kołowego jest równe różnicy pól dużego i małego koła, czyli
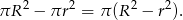
Aby zobaczyć, że wartość ta zależy tylko od cięciwy 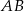 , popatrzmy na trójkąt prostokątny
, popatrzmy na trójkąt prostokątny 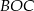 .
.
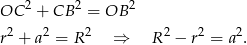
Zatem pole pierścienia jest równe
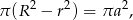
co pokazuje, że zależy ono tylko od długości cięciwy.

