Zadanie nr 7902218
W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość 10 i jest styczna do wewnętrznego okręgu (zobacz rysunek).
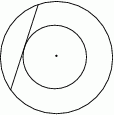
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
Rozwiązanie
Dorysujmy promienie okręgów.
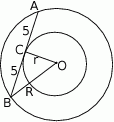
Pole pierścienia kołowego jest równe różnicy pól dużego i małego koła, czyli
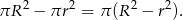
Korzystając z twierdzenia Pitagorasa w trójkącie prostokątnym 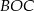 , mamy
, mamy
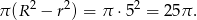
Zatem pole pierścienia rzeczywiście nie zależy od promieni okręgów.

