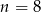/Szkoła średnia/Prawdopodobieństwo/Z definicji/Losy

Zadanie nr 2009229

Na loterii jest n losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby n prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe 1114 ?

Wersja PDF

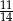Rozwiązanie

Dwa losy z n możemy wybrać na

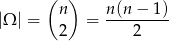
(n ) n(n − 1 ) |Ω | = = --------- 2 2

sposobów.

Policzmy najpierw zdarzenia sprzyjające, w których mamy dwa losy wygrywające. Jest ich

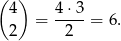
( ) 4 4-⋅3 2 = 2 = 6.

Jeżeli jest dokładnie jeden los wygrywający to możemy go wybrać na 4 sposoby i do tego dobieramy los przegrywający, co możemy zrobić na 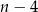n− 4 sposoby.

Zatem interesujące nas prawdopodobieństwo jest równe

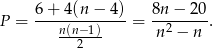
6-+-4(n-−-4-) 8n-−-2-0 P = n(n−-1) = n2 − n . 2

Musimy więc rozwiązać równanie

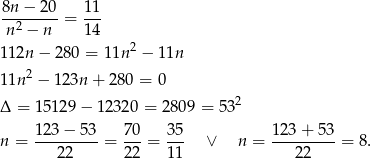
8n − 20 11 --2-----= --- n − n 14 112n − 280 = 11n2 − 11n 2 11n − 123n + 2 80 = 0 Δ = 15 129 − 12320 = 2809 = 532 n = 12-3−--53 = 7-0 = 3-5 ∨ n = 123-+-53-= 8. 2 2 2 2 1 1 22

Zatem 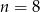n = 8 .  
Odpowiedź: n = 8

Wersja PDF