Zadanie nr 3822939
Na loterię przygotowano 30 losów, z których  jest wygrywających. Kupujemy 2 razy po jednym losie. Wyznacz
jest wygrywających. Kupujemy 2 razy po jednym losie. Wyznacz  , jeśli wiadomo, że prawdopodobieństwo kupienia w ten sposób dwóch losów wygrywających jest równe
, jeśli wiadomo, że prawdopodobieństwo kupienia w ten sposób dwóch losów wygrywających jest równe 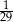 .
.
Rozwiązanie
Sposób I
Zastanówmy się jakie jest prawdopodobieństwo, że pierwszy los jest wygrywający. Mamy trzydzieści losów (to jest nasza 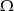 ) spośród których
) spośród których  jest wygrywających, czyli prawdopodobieństwo wynosi
jest wygrywających, czyli prawdopodobieństwo wynosi
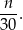
Teraz zastanówmy się jakie jest prawdopodobieństwo, że drugi jest wygrywający. Po pierwszym losowaniu zostało nam 29 losów w tym 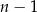 losów wygrywających (bo wylosowaliśmy jeden los wygrywający wcześniej). Zatem prawdopodobieństwo wynosi
losów wygrywających (bo wylosowaliśmy jeden los wygrywający wcześniej). Zatem prawdopodobieństwo wynosi
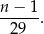
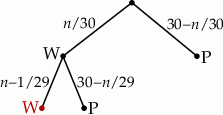
Naszą sytuację możemy przedstawić na drzewku
Zatem otrzymujemy równanie
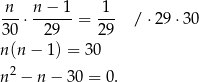
Liczymy wyróżnik i pierwiastki
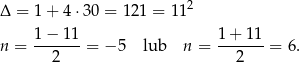
Odrzucamy rozwiązanie ujemny i otrzymujemy, że 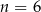 .
.
Sposób II
Parę losów możemy wybrać na
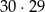
sposobów (uwzględniamy kolejność), a parę dwóch losów wygrywających na
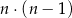
sposobów (pierwszy los na  sposobów, a drugi na
sposobów, a drugi na 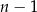 ). Mamy więc równanie
). Mamy więc równanie
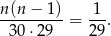
Rozwiązujemy je dokładnie tak samo jak w I sposobie.
Odpowiedź: