/Szkoła średnia/Prawdopodobieństwo/Z definicji/Losy

Zadanie nr 8811616

Dodaj do ulubionych
Dodaj do rozwiązanych

W pierwszej loterii jest 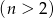n (n > 2) losów, spośród których jeden wygrywa, a w drugiej jest 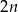2n losów, spośród których dwa wygrywają. Gracz chce kupić dwa losy w jednej z tych loterii. W której z nich ma większą szansę otrzymania co najmniej jednego losu wygrywającego?

Rozwiązanie

Policzmy oba prawdopodobieństwa.

W pierwszej loterii możemy wybrać dwa losy na

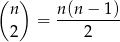
( ) n = n(n-−-1)- 2 2

sposoby. Zdarzeń sprzyjających jest 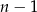n − 1 (trzeba wybrać los wygrywający i jeszcze jeden przegrywający), czyli

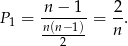
n-−-1-- 2- P1 = n(n−1) = n. 2

W drugiej loterii dwa losy można wybrać na

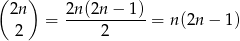
( 2n ) 2n(2n − 1 ) = -----------= n(2n − 1 ) 2 2

sposoby. Zdarzeń sprzyjających jest: 1 (oba losy wygrywające)+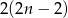2(2n − 2) (na dwa sposoby możemy wybrać los wygrywający i na 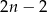2n − 2 sposobów dobrać do niego los przegrywający). Zatem

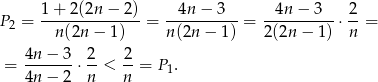
1+--2(2n-−-2)- -4n-−--3-- --4n-−-3-- 2- P2 = n(2n − 1) = n(2n − 1 ) = 2(2n − 1) ⋅ n = = 4n−--3-⋅ 2-< 2-= P . 4n− 2 n n 1

 
Odpowiedź: W pierwszej

Wersja PDF