Zadanie nr 3011412

Wykazać, że jeśli 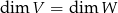dim V = d im W , to z tego, że odwzorowanie liniowe 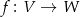f : V → W jest różnowartościowe wynika, że 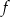jest izomorﬁzmem.

Rozwiązanie

Sposób I

Skorzystamy ze wzoru

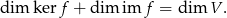
d im ker f + dim im f = dim V .

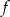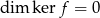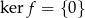Ponieważ jest różnowartościowe to dim ke rf = 0 (bo k erf = { 0} ), zatem

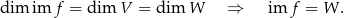
d im im f = d im V = dim W ⇒ im f = W .

Czyli 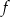jest „na”. Jest więc odwracalnym odwzorowaniem liniowym, czyli izomorﬁzmem. Jeżeli ktoś nie zauważył, to skorzystaliśmy z faktu, że jeżeli 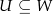U ⊆ W podprzestrzeń liniowa i 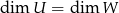d im U = dim W to U = W .

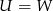Sposób II

Możemy też uzasadnić to bardziej bezpośrednio. Łatwo jest wykazać, że jeżeli odwzorowanie liniowe 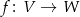f : V → W jest różnowartościowe to przeprowadza układy liniowo niezależne w 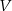na układy niezależne w 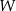. Z tego wynika, że jeżeli dodatkowo 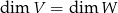dim V = dim W to 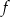przeprowadza bazę na bazę. Zatem 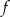jest na (bo obraz 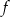jest podprzestrzenią liniową 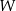oraz zawiera jej bazę, czyli musi być całym 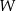). Zatem 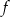jest izomorﬁzmem.