/Studia/Algebra liniowa/Odwzorowania liniowe

Zadanie nr 6050294

Dodaj do ulubionych
Dodaj do rozwiązanych

Załóżmy, że odwzorowanie liniowe 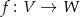f : V → W jest różnowartościowe.

  • Wykazać, że 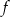f przekształca układ wektorów liniowo niezależnych w 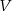V na układ wektorów liniowo niezależnych w W .
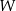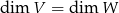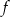  • Wykazać, że jeśli d im V = dim W to f przekształca bazę w 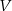V na bazę w W .

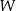Rozwiązanie

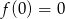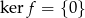Skorzystamy ze znanego faktu, że f(0 ) = 0 , czyli w przypadku odwzorowania różnowartościowego mamy kerf = {0} .

  • Niech 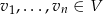v1,...,vn ∈ V będzie układem liniowo niezależnym i załóżmy, że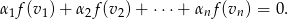
    α1f(v 1)+ α 2f(v2)+ ⋅⋅⋅+ αnf (vn) = 0.

    Musimy pokazać, że 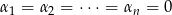α1 = α2 = ⋅⋅⋅ = αn = 0 . Ponieważ 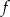f jest liniowe i ma trywialne jądro, mamy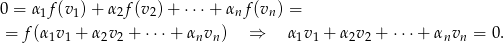

    0 = α 1f(v1) + α2f(v 2)+ ⋅⋅⋅ + αnf (vn) = = f (α1v1 + α2v2 + ⋅⋅⋅+ αnvn) ⇒ α 1v1 + α2v2 + ⋅⋅⋅+ αnvn = 0.

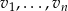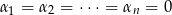    Pozostało skorzystać z tego, że układ v1,...,vn jest liniowo niezależny, zatem α 1 = α2 = ⋅⋅⋅ = αn = 0 .

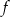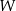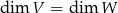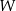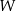  • Baza to maksymalny układ liniowo niezależny. Z poprzedniego podpunktu wiemy, że f przekształca taki układ na układ liniowo niezleżny w W , który ma tyle samo elementów. Jeżeli d im V = dim W , to ten układ jest maksymalny w W , jest więc bazą W .
Wersja PDF