Definicje Ciąg to po prostu ponumerowany zbiór elementów, np.

W powyższym przykładzie 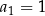 jest pierwszym elementem ciągu,
jest pierwszym elementem ciągu, 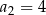 drugim itd. Jeżeli nie chcemy przy każdym wyrazie pisać
drugim itd. Jeżeli nie chcemy przy każdym wyrazie pisać  itd. możemy użyć zapisu
itd. możemy użyć zapisu
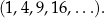
W takim zapisie domyślnie 1 jest pierwszym elementem ciągu, 4 drugim, 9 trzecim itd.
Jeżeli chcemy się odwołać do ciągu, ale bez precyzowania ile są równe jego elementy, na ogół piszemy 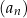 lub
lub 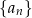 .
.
Ciąg jest skończony, jeżeli ma tylko skończenie wiele elementów, albo nieskończony w przeciwnym wypadku. Jeżeli chcemy zaznaczyć w notacji 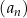 , że ciąg ma skończenie wiele wyrazów to piszemy
, że ciąg ma skończenie wiele wyrazów to piszemy 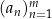 . Zapis ten czytamy: ciąg
. Zapis ten czytamy: ciąg 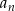 , gdzie
, gdzie  zmienia się od 1 do
zmienia się od 1 do 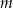 . Zapis ten należy rozumieć jako skrót zapisu
. Zapis ten należy rozumieć jako skrót zapisu

Jeżeli chcemy zaznaczyć, że ciąg jest nieskończony to piszemy 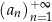 i czytamy: ciąg
i czytamy: ciąg 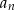 , gdzie
, gdzie  zmienia się od 1 do nieskończoności. Jest skrót zapisu
zmienia się od 1 do nieskończoności. Jest skrót zapisu

Jeżeli wprowadzimy na płaszczyźnie układ współrzędnych, to o każdym punkcie płaszczyzny możemy myśleć jak o dwuelementowym ciągu 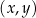 jego współrzędnych.
jego współrzędnych.
Podobnie, punkty przestrzeni możemy traktować jako trójelementowe ciągi ich współrzędnych: 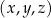 .
.
Formalnie ciąg definiuje się jako dowolną funkcję, której dziedziną jest zbiór liczb naturalnych 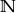 , w przypadku ciągu nieskończonego, oraz zbiór
, w przypadku ciągu nieskończonego, oraz zbiór 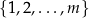 , w przypadku ciągu skończonego o
, w przypadku ciągu skończonego o 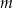 wyrazach. Powinno być jasne, że jest to tylko ’mądry’ zapis naszego powyższego opisu. Jeżeli traktujemy ciąg jako funkcję, to
wyrazach. Powinno być jasne, że jest to tylko ’mądry’ zapis naszego powyższego opisu. Jeżeli traktujemy ciąg jako funkcję, to 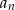 jest skrótowym zapisem wartości funkcji
jest skrótowym zapisem wartości funkcji 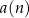 . Różne sposoby określania ciągu Podobnie jak funkcje, ciągi można definiować na wiele róznych sposobów.
. Różne sposoby określania ciągu Podobnie jak funkcje, ciągi można definiować na wiele róznych sposobów.
1. Wypisując wyrazy ciągu.
Wypiszmy kilka ciągów skończonych.
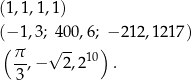
W drugim z powyższych przykładów celowo użyliśmy średnika do rozdzielenia kolejnych wyrazów ciągu, żeby uniknąć pomyłki z przecinkiem rozdzielającym miejsca dzisiętne.
Oczywiście nie da się wypisać wszystkich wyrazów ciągu nieskończonego, ale często używa się zapisów typu
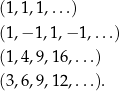
W takich sytuacjach oczekuje się, że czytelnik jest wystarczająco spostrzegawczy, żeby domyślić się jaki nieskończony ciąg mamy na myśli. W pierwszym przykładzie mamy na myśli ciąg, którego wszystkie wyrazy są równe 1; w drugim ciąg, w którym na przemian są 1 i -1; w trzecim ciąg kolejnych kwadratów liczb naturalnych; w czwartym ciąg kolejnych liczb naturalnych podzielnych przez 3.
2. Opisem słownym.
Często podajemy pewną własność, która w pełni wyznacza ciąg.
Ciąg dwucyfrowych kwadratów liczb naturalnych to ciąg
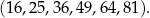
Ciąg kolejnych dodatnich liczb całkowitych parzystych to ciąg
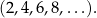
Wyznaczmy wzór ciągu 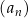 kolejnych liczb naturalnych, które przy dzieleniu przez 7 dają resztę 3.
kolejnych liczb naturalnych, które przy dzieleniu przez 7 dają resztę 3.
Oczywiście chodzi o ciąg
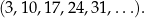
Wzór tego ciągu to
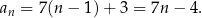
Zauważmy, że nie jest to ciąg 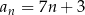 (bo
(bo 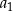 ma być równe 3, a nie 10).
ma być równe 3, a nie 10).
3. Wzorem.
Obliczmy kilka początkowych wyrazów ciągu 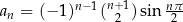 .
.
Liczymy
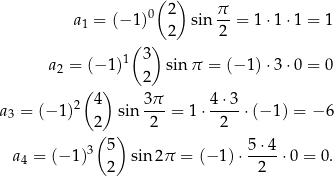
i tak dalej.
4. Rekurencyjnie.
Tej metodzie poświęcimy cały następny rozdział. Ciągi zdefiniowane rekurencyjnie Rekurencyjna definicja ciągu zawsze składa się z dwóch elementów:
-
wartości pierwszego (lub kilku pierwszych) wyrazów ciągu;
-
reguły, która jednoznacznie opisuje w jaki sposób powstają kolejne wyrazy ciągu.
Regułę, o której mowa w drugim punkcie zwykle nazywa się zależnością rekurencyjną definiującą ciąg. Na ogół jest to przepis (wzór) pozwalający wyliczyć  -ty wyraz ciągu, jeżeli znamy już wyrazy o numerach mniejszych od
-ty wyraz ciągu, jeżeli znamy już wyrazy o numerach mniejszych od  .
.
Spróbujmy wyznaczyć wzór ciągu określonego przez warunki 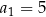 oraz
oraz 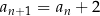 , dla
, dla 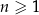 .
.
Z podanej zależności rekurencyjnej wyliczamy kolejne wyrazy ciągu (podstawiamy kolejno 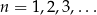 ).
).
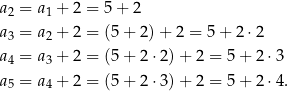
Powinniśmy się już domyślić ile będzie równy  -ty wyraz ciągu:
-ty wyraz ciągu: 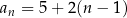 .
.
Zauważmy, że na razie jedynie zgadliśmy wzór na  . Jeżeli chcemy uzasadnić poprawność tej obserwacji (żeby mieć pewność, że się nie pomyliliśmy), musimy skorzystać z indukcji. Sprawdzamy, że dla
. Jeżeli chcemy uzasadnić poprawność tej obserwacji (żeby mieć pewność, że się nie pomyliliśmy), musimy skorzystać z indukcji. Sprawdzamy, że dla 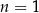 nasz wzór daje prawidłową wartość
nasz wzór daje prawidłową wartość 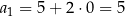 , oraz że spełniony jest krok indukcyjny
, oraz że spełniony jest krok indukcyjny
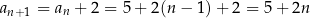
(założyliśmy wyżej, że  i korzystając z podanej rekurencji uzasadniliśmy, że
i korzystając z podanej rekurencji uzasadniliśmy, że 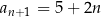 ).
).
Wyznaczmy wzór ciągu określonego przez warunki 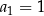 oraz
oraz
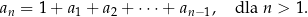
Liczymy kolejne wyrazy ciągu 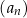
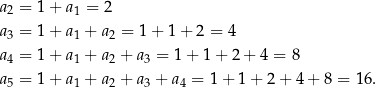
Widać już co jest grane? Zgadujemy, że 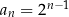 i uzasadniamy to indukcyjnie. Dla
i uzasadniamy to indukcyjnie. Dla 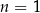 mamy
mamy  . Zanim wykonamy krok indukcyjny, uprośćmy trochę podaną rekurencję:
. Zanim wykonamy krok indukcyjny, uprośćmy trochę podaną rekurencję:
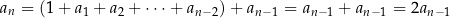
(skorzystaliśmy dwa razy z rekurencji, raz dla 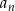 i raz dla
i raz dla 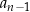 ). Teraz łatwo wykonać krok indukcyjny
). Teraz łatwo wykonać krok indukcyjny
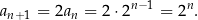
Ciągi jako funkcje Mówiliśmy już, że ciągi definiuje się jako funkcje o bardzo specjalnej dziedzinie: 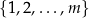 lub
lub 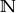 . W takim razie ciągi dziedziczą od funkcji wiele różnych cech, np. jest sens mówić o wykresie ciągu. Wykres ciągu zawsze będzie składał się pojedynczych punktów zaznaczonych nad kolejnymi liczbami naturalnymi. Punktów będzie skończenie wiele, gdy ciąg jest skończony oraz nieskończenie wiele, gdy ciąg jest nieskończony.
. W takim razie ciągi dziedziczą od funkcji wiele różnych cech, np. jest sens mówić o wykresie ciągu. Wykres ciągu zawsze będzie składał się pojedynczych punktów zaznaczonych nad kolejnymi liczbami naturalnymi. Punktów będzie skończenie wiele, gdy ciąg jest skończony oraz nieskończenie wiele, gdy ciąg jest nieskończony.
Naszkicujmy wykres ciągu 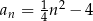 .
.
Szkicujemy.

Kolejna własność analogiczna jak dla funkcji to monotoniczność. Mówimy, że ciąg 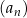 jest rosnący jeżeli dla każdego
jest rosnący jeżeli dla każdego  spełniona jest nierówność
spełniona jest nierówność
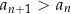
(każdy kolejny wyraz jest większy od poprzedniego). Jeżeli nierówność jest słaba, czyli

to mówimy, że ciąg 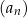 jest niemalejący (wyrazy nie maleją).
jest niemalejący (wyrazy nie maleją).
Analogicznie mówimy, że ciąg 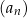 jest malejący (nierosnący) jeżeli
jest malejący (nierosnący) jeżeli
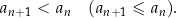
Zwyczajowo przez ciąg monotoniczny rozumie się ciąg rosnący lub malejący. Jeżeli jednak chcemy też dopuścić ciągi niemalejące i nierosnące to zwykle używa się terminu ciąg słabo monotoniczny (co wskazuje na to, że nierówność może być słaba).
Zbadajmy monotoniczność ciągu 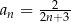 .
.
Liczymy różnicę 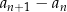 kolejnych wyrazów ciągu. Jeżeli wyjdzie dodatnia to będzie znaczyło, że ciąg jest rosnący, a jeżeli wyjdzie ujemna, że jest malejący.
kolejnych wyrazów ciągu. Jeżeli wyjdzie dodatnia to będzie znaczyło, że ciąg jest rosnący, a jeżeli wyjdzie ujemna, że jest malejący.
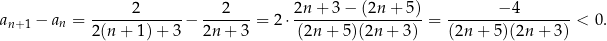
Zatem ciąg jest malejący.
Zbadajmy monotoniczność ciągu 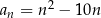 .
.
Jak poprzednio, liczmy różnicę
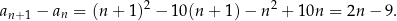
No i mamy kłopot, bo nie jesteśmy w stanie ustalić jaki jest znak otrzymanego wyrażania (zależy on od  ). W takim razie ciąg nie jest monotoniczny. Zauważmy jednak, że jeżeli
). W takim razie ciąg nie jest monotoniczny. Zauważmy jednak, że jeżeli 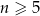 to
to 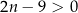 i ciąg zaczyna być rosnący. W takiej sytuacji często pisze się, że ciąg jest rosnący począwszy od 5 wyrazu. Tego typu odpowiedź jest oczywiście o wiele treściwsza niż krótkie ciąg nie jest monotoniczny.
i ciąg zaczyna być rosnący. W takiej sytuacji często pisze się, że ciąg jest rosnący począwszy od 5 wyrazu. Tego typu odpowiedź jest oczywiście o wiele treściwsza niż krótkie ciąg nie jest monotoniczny.
Gdy pomyślimy sobie o wykresie ciągu  to powinno być jasne, że ciąg ten nie będzie monotoniczny, niezależnie od tego jak duże jest
to powinno być jasne, że ciąg ten nie będzie monotoniczny, niezależnie od tego jak duże jest  .
.

W takiej sytuacji, na pytanie o monotoniczność nie ma mądrzejszej odpowiedzi niż ciąg nie jest monotoniczny.

