/Studia/Analiza/Ciągi/Różne

Zadanie nr 4047253

Zbadaj, czy ciąg 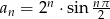n nπ- an = 2 ⋅sin 2 jest ograniczony z góry, z dołu, lub ograniczony.

Wersja PDF

Rozwiązanie

Dla 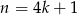n = 4k + 1 mamy

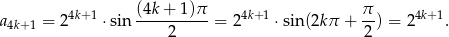
(4k + 1)π π a4k+1 = 24k+ 1 ⋅sin---------- = 24k+1 ⋅sin(2kπ + --) = 24k+1. 2 2

A dla n = 4k + 3

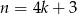
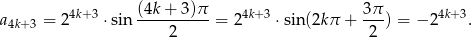
a = 24k+3 ⋅sin (4k-+-3-)π = 24k+ 3 ⋅sin(2k π + 3π-) = −2 4k+ 3. 4k+3 2 2

Widać zatem, że ciąg nie jest ograniczony z dołu i nie jest ograniczony z góry.  
Odpowiedź: Nie jest ograniczony, ani z dołu, ani z góry.

Wersja PDF