Zadanie nr 7729670
Zbadaj, czy ciąg 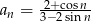 jest ograniczony z góry, z dołu, lub ograniczony.
jest ograniczony z góry, z dołu, lub ograniczony.
Rozwiązanie
Korzystamy z tego, że ![sin n,co sn ∈ [− 1,1]](https://img.zadania.info/zad/7729670/HzadR0x.gif) .
.
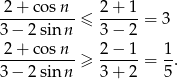
Odpowiedź: Ciąg jest ograniczony.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Zbadaj, czy ciąg 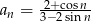 jest ograniczony z góry, z dołu, lub ograniczony.
jest ograniczony z góry, z dołu, lub ograniczony.
Korzystamy z tego, że ![sin n,co sn ∈ [− 1,1]](https://img.zadania.info/zad/7729670/HzadR0x.gif) .
.
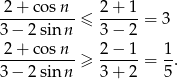
Odpowiedź: Ciąg jest ograniczony.
