/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z logarytmiczną

Zadanie nr 1501659

Dziedziną funkcji 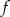f opisanej wzorem 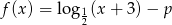f (x) = log 12(x+ 3)− p jest przedział 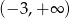(− 3,+ ∞ ) . Wiedząc, że do wykresu funkcji 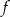f należy punkt 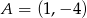A = (1,− 4) , oblicz wartość parametru 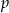p . Następnie:

  • naszkicuj wykres funkcji g (x) = |f(x)| ;
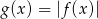  • wyznacz zbiór wszystkich wartości parametru 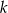k , dla których równanie 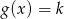g(x) = k ma dwa rozwiązania różnych znaków.
Wersja PDF

Rozwiązanie

Podstawiamy współrzędne danego punktu 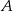A do wzoru funkcji, aby wyliczyć p .

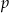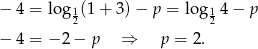
− 4 = log 12(1+ 3 )− p = log12 4− p − 4 = − 2 − p ⇒ p = 2.

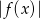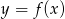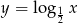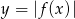Możemy teraz naszkicować wykres funkcji |f(x)| . Wykres funkcji y = f (x) otrzymujemy z wykresu y = lo g1 x 2 przez przesunięcie o wektor [− 3,− 2] , a wykres y = |f (x)| otrzymamy odbijając część poniżej osi 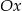Ox do góry.

PIC

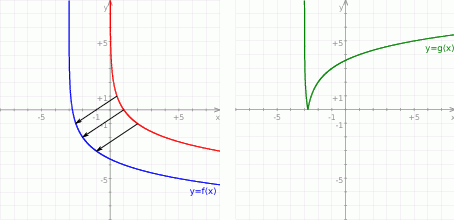
Z obrazka widać, że jeżeli tylko 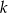k jest większe niż druga współrzędna punktu wspólnego wykresu funkcji 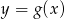y = g(x ) oraz osi 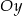Oy to dane równanie ma dwa rozwiązania różnych znaków. Punkt ten to po prostu 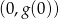(0,g(0 )) , czyli

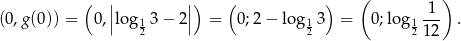
( ) ( || ||) ( ) 1 (0,g (0)) = 0,|log 13 − 2| = 0;2 − log1 3 = 0;log 1--- . 2 2 21 2

Zatem równanie ma dwa rozwiązania różnych znaków dla 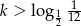k > log 1112 2 .  
Odpowiedź: 1- p = 2, k > lo g12 12

Wersja PDF