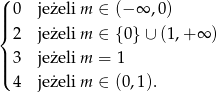/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z logarytmiczną

Zadanie nr 7846087

Dodaj do ulubionych
Dodaj do rozwiązanych

Na rysunku przedstawiony jest fragment wykresu funkcji określonej wzorem 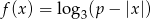f (x) = log3(p − |x|) .

PIC

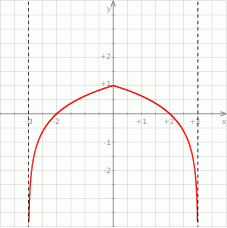
  • Podaj wartość p .
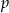  • Naszkicuj wykres funkcji y = |f(x )| .
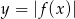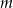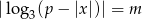  • Podaj w zależności od parametru m liczbę rozwiązań równania |log3(p − |x|)| = m .

Rozwiązanie

  •  

    Sposób I

    Zauważmy, że dziedziną funkcji 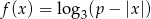f (x) = log (p − |x|) 3 jest zbiór rozwiązań nierówności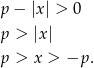

    p − |x| > 0 p > |x | p > x > −p .

    Z drugiej strony, dziedziną funkcji przedstawionej na wykresie jest przedział 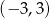(− 3,3) , więc p = 3 .

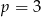    Sposób II

    Z obrazka widać, że punkt 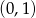(0,1) należy do wykresu funkcji, więc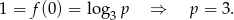

    1 = f(0) = log p ⇒ p = 3. 3

     
    Odpowiedź: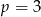 p = 3

  • Wykres funkcji 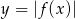y = |f(x)| otrzymujemy z wykresu funkcji 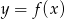y = f(x) odbijając część wykresu znajdującą się poniżej osi 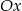Ox do góry.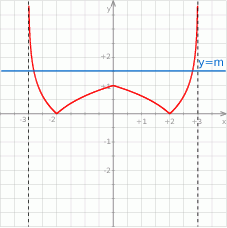
    PIC
  • Odczytujemy z wykresu – liczba rozwiązań danego równania wynosi
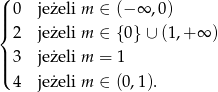
    (| 0 jeżeli m ∈ (−∞ ,0 ) ||{ 2 jeżeli m ∈ {0} ∪ (1,+ ∞ ) || 3 jeżeli m = 1 |( 4 jeżeli m ∈ (0,1).

     
    Odpowiedź: ( |||{ 0 jeżeli m ∈ (− ∞ ,0) 2 jeżeli m ∈ {0} ∪ (1,+ ∞ ) | 3 jeżeli m = 1 ||( 4 jeżeli m ∈ (0,1).

Wersja PDF