/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z logarytmiczną

Zadanie nr 9627985

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 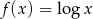f(x ) = lo gx .

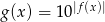  • Naszkicuj wykres funkcji g(x) = 10|f(x)| .
  • Udowodnij, że jeżeli 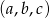(a,b,c) jest ciągiem geometrycznym o wyrazach dodatnich to 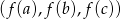(f(a),f(b ),f (c)) jest ciągiem arytmetycznym.

Rozwiązanie

  • Oczywiście dziedziną funkcji 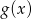g(x ) jest zbiór 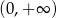(0,+ ∞ ) , ponadto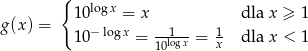
    { 10 logx = x dla x ≥ 1 g (x) = −logx --1-- 1 10 = 10logx = x dla x < 1

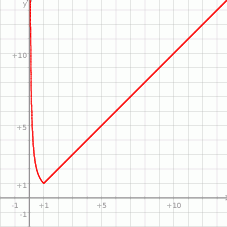
    Teraz bez trudu szkicujemy wykres funkcji g (x) .

    PIC
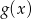  • Z podanych informacji wiemy, że 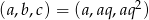(a,b,c) = (a,aq ,aq2) dla pewnego 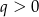q > 0 . Zatem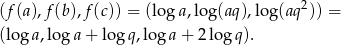
    2 (f(a ),f (b),f(c)) = (log a,lo g(aq),log(aq )) = (log a,lo ga + log q,loga + 2 logq ).

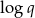    Widać, że jest to ciąg arytmetyczny o różnicy logq .

Wersja PDF