Zadanie nr 1533554
Jedno z rozwiązań równania 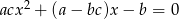 z niewiadomą
z niewiadomą  jest równe 4. Liczby
jest równe 4. Liczby 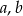 i
i  (w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
(w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
Rozwiązanie
Ponieważ 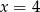 jest pierwiastkiem, mamy
jest pierwiastkiem, mamy
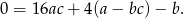
Ponadto
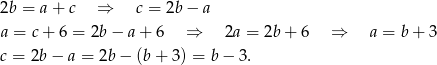
Podstawiamy teraz wyliczone 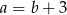 i
i 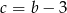 do pierwszego z otrzymanych równań.
do pierwszego z otrzymanych równań.
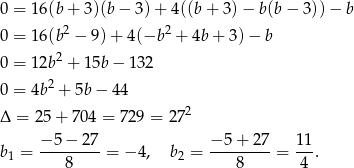
Mamy wtedy odpowiednio
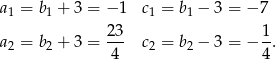
Drugi pierwiastek obliczamy ze wzoru Viète’a
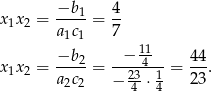
Zatem drugi pierwiastek jest równy odpowiednio
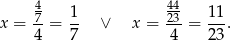
Odpowiedź: 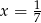 lub
lub