/Szkoła średnia/Ciągi/Arytmetyczny/Trzywyrazowy

Zadanie nr 2284886

Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór wszystkich punktów płaszczyzny o współrzędnych 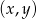(x,y) , dla których ciąg: 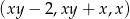(xy − 2 ,xy+ x,x) jest rosnącym ciągiem arytmetycznym.

Wersja PDF

Rozwiązanie

Jeżeli podane trzy liczby mają tworzyć ciąg arytmetyczny to musi być spełniony warunek

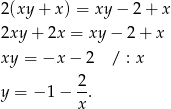
2(xy + x) = xy − 2 + x 2xy + 2x = xy − 2+ x xy = −x − 2 / : x 2- y = − 1− x.

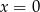Po drodze podzieliliśmy przez x , ale nie ma z tym problemu, bo dla x = 0 otrzymujemy sprzeczną równość 0 = − 2 .

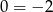To jednak nie koniec, bo jeszcze nie skorzystaliśmy z informacji o tym, że mamy mieć rosnący ciąg arytmetyczny. Tak będzie gdy

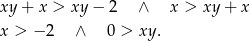
xy + x > xy− 2 ∧ x > xy+ x x > − 2 ∧ 0 > xy.

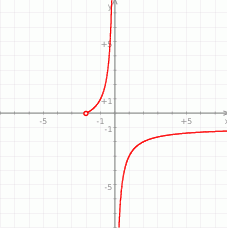
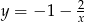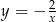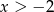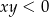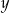Wykresem funkcji y = − 1− 2 x jest hiperbola y = − -2 x przesunięta o 1 jednostkę w dół. Rysujemy jednak tylko fragment wykresu dla x > −2 . Zauważmy, że w tej sytuacji jest też spełniony warunek xy < 0 (liczby x i y mają różne znaki).

PIC

Wersja PDF