Zadanie nr 3568056
Dla jakich wartości parametru 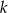 równanie
równanie 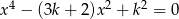 ma co najmniej trzy różne pierwiastki, które są kolejnymi wyrazami ciągu arytmetycznego?
ma co najmniej trzy różne pierwiastki, które są kolejnymi wyrazami ciągu arytmetycznego?
Rozwiązanie
Sposób I
Równanie jest dwukwadratowe, podstawmy więc 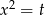 .
.
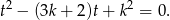
Aby wyjściowe równanie miało co najmniej trzy pierwiastki, powyższe równanie kwadratowe musi mieć dwa pierwiastki dodatnie 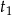 i
i 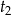 . Wtedy rozwiązania oryginalnego równania to
. Wtedy rozwiązania oryginalnego równania to 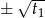 i
i 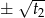 . Kiedy trzy z tych liczb mogą tworzyć ciąg arytmetyczny? Wśród tych trzech liczb na pewno są dwie przeciwne, powiedzmy, że
. Kiedy trzy z tych liczb mogą tworzyć ciąg arytmetyczny? Wśród tych trzech liczb na pewno są dwie przeciwne, powiedzmy, że 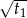 i
i 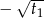 . Mamy wtedy następujące możliwości na kolejność w jakiej liczby tworzą ciąg arytmetyczny.
. Mamy wtedy następujące możliwości na kolejność w jakiej liczby tworzą ciąg arytmetyczny.
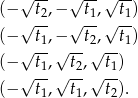
Korzystając z faktu, że liczby 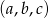 tworzące ciąg arytmetyczny spełniają równość
tworzące ciąg arytmetyczny spełniają równość 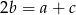 , mamy kolejno
, mamy kolejno
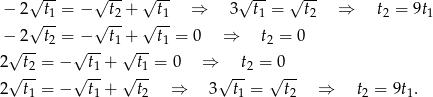
Na początek sprawdźmy kiedy  jest rozwiązaniem równania
jest rozwiązaniem równania 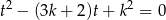 .
.
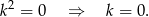
Równanie ma wtedy postać
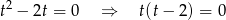
i wyjściowe równanie ma pierwiastki
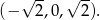
Pozostało sprawdzić, kiedy równanie 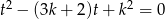 ma dwa dodatnie pierwiastki spełniające równość
ma dwa dodatnie pierwiastki spełniające równość 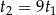 . Korzystając ze wzorów na pierwiastki mamy
. Korzystając ze wzorów na pierwiastki mamy
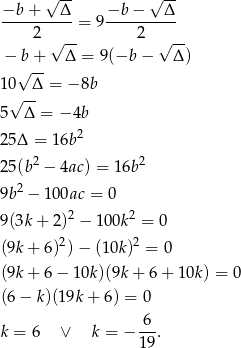
Otrzymane wartości 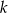 trzeba sprawdzić – po drodze równanie podnosiliśmy do kwadratu, więc mogły się pojawić jakieś fałszywe rozwiązania.
trzeba sprawdzić – po drodze równanie podnosiliśmy do kwadratu, więc mogły się pojawić jakieś fałszywe rozwiązania.
Dla 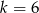 jest to w miarę proste. Mamy równanie
jest to w miarę proste. Mamy równanie
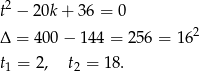
Zatem wśród pierwiastków wyjściowego równania jest trójka 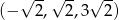 .
.
Dla 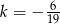 mamy
mamy
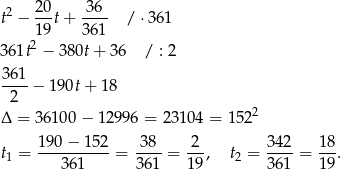
Zatem wśród rozwiązań wyjściowego równania są liczby
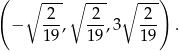
Zamiast powyższego sprawdzenia, mogliśmy wrócić do wyliczenia  , i zastanowić się, w którym miejscu przejście między równaniami nie było równoważnością. Był tylko jeden taki moment, gdy podnosiliśmy równanie do kwadratu
, i zastanowić się, w którym miejscu przejście między równaniami nie było równoważnością. Był tylko jeden taki moment, gdy podnosiliśmy równanie do kwadratu
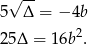
Kiedy to przejście jest równoważnością (tzn. nie dokładamy żadnych dodatkowych pierwiastków)? – jeżeli wiemy, że obie strony są dodatnie. Lewa jest, a prawa jest, o ile 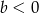 – tak jednak jest zarówno dla
– tak jednak jest zarówno dla 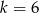 jak i
jak i 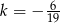 .
.
Sposób II
Powiedzmy, że te trzy pierwiastki to 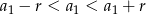 . Daje to nam układ równań
. Daje to nam układ równań
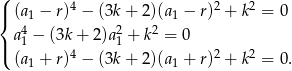
Na początek spróbujmy pozbyć się którejś niewiadomej – najłatwiej jest wyeliminować 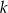 . Odejmijmy od pierwszego równania drugie.
. Odejmijmy od pierwszego równania drugie.
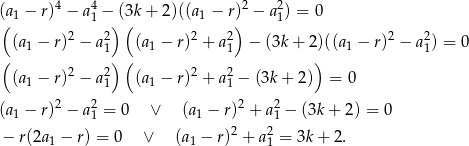
Zanim się dokładnie tym warunkom przyjrzymy, zróbmy to samo dla równań trzeciego i drugiego
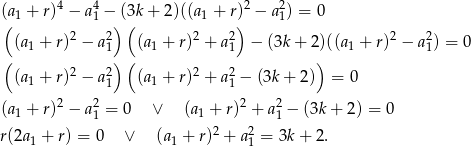
Zauważmy, że ponieważ wyrazy ciągu mają być różne to 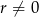 , zatem pierwsza możliwość daje nam
, zatem pierwsza możliwość daje nam 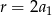 i dwa ostatnie równania przyjmują postać.
i dwa ostatnie równania przyjmują postać.
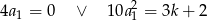
Pierwsza równość implikuje 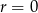 , więc mamy
, więc mamy 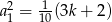 i drugie równanie początkowego układu przyjmuje postać
i drugie równanie początkowego układu przyjmuje postać
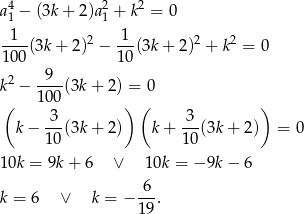
Dobrze, bierzemy się za drugi możliwy przypadek, czyli
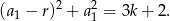
Patrząc na następną parę równań, mamy dwie możliwości. Jeżeli 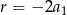 to podobnie jak poprzednio, z powyższego równania mamy
to podobnie jak poprzednio, z powyższego równania mamy 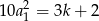 i mamy dokładnie te same rachunki, które już zrobiliśmy.
i mamy dokładnie te same rachunki, które już zrobiliśmy.
Załóżmy zatem, że 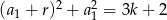 . Mamy wtedy
. Mamy wtedy
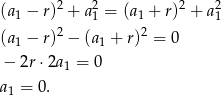
Teraz drugie równanie układu przyjmuje postać
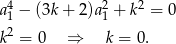
Odpowiedź: