/Szkoła średnia/Ciągi/Arytmetyczny/Trzywyrazowy

Zadanie nr 4682085

Dodaj do ulubionych
Dodaj do rozwiązanych

Współczynniki 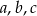a,b,c funkcji kwadratowej 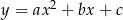2 y = ax + bx + c w podanej kolejności tworzą ciąg arytmetyczny. Jednym z miejsc zerowych tej funkcji jest 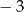− 3 . Punkt o współrzędnych 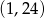(1,24) należy do wykresu funkcji. Znajdź drugie miejsce zerowe oraz wartości współczynników a,b,c .

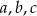Rozwiązanie

Wiemy, że

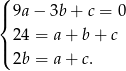
( |{ 9a − 3b + c = 0 24 = a+ b+ c |( 2b = a+ c.

Podstawiamy 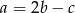a = 2b− c z trzeciego równania do dwóch pierwszych i mamy

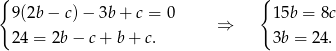
{ { 9(2b− c)− 3b+ c = 0 15b = 8c 24 = 2b − c + b + c. ⇒ 3b = 24.

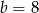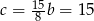Zatem b = 8 i 15 c = 8 b = 15 . Stąd

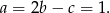
a = 2b− c = 1.

Pozostało wyznaczyć drugi pierwiastek równania

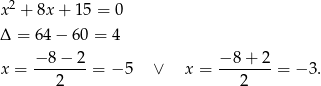
2 x + 8x + 15 = 0 Δ = 64 − 60 = 4 − 8− 2 − 8+ 2 x = ------- = − 5 ∨ x = ------- = − 3. 2 2

 
Odpowiedź: x2 = −5 ,(a ,b,c) = (1,8,15)

Wersja PDF