/Szkoła średnia/Ciągi/Arytmetyczny/Trzywyrazowy

Zadanie nr 6375134

Dla jakich 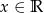x ∈ R liczby 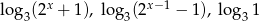x x−1 lo g3(2 + 1), log 3(2 − 1), log 31 tworzą, w podanej kolejności, ciąg arytmetyczny. Wyznacz różnicę tego ciągu.

Wersja PDF

Rozwiązanie

Nie będziemy na razie przejmować się dziedziną równania, po prostu sprawdzimy otrzymane rozwiązania. Trzy liczby 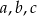a,b,c tworzą ciąg arytmetyzny jeżeli 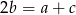2b = a + c . Mamy zatem równanie

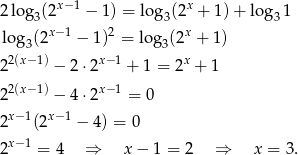
2log3(2x− 1 − 1 ) = lo g3(2x + 1)+ lo g31 x− 1 2 x log3(2 − 1) = lo g3(2 + 1) 22(x− 1) − 2 ⋅2x−1 + 1 = 2x + 1 22(x− 1) − 4 ⋅2x−1 = 0 x−1 x− 1 2 (2 − 4) = 0 2x−1 = 4 ⇒ x− 1 = 2 ⇒ x = 3.

Dane liczby to wtedy 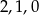2,1,0 , zatem różnica wynosi − 1 .  
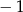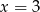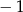Odpowiedź: x = 3 , różnica: − 1 .

Wersja PDF