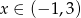Zadanie nr 8677691
Liczby 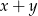 ,
, 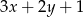 i
i 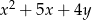 tworzą ciąg arytmetyczny. Wyznacz te wartości
tworzą ciąg arytmetyczny. Wyznacz te wartości  , dla których ciąg ten jest rosnący.
, dla których ciąg ten jest rosnący.
Rozwiązanie
Trzy liczby 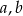 i
i  tworzą ciąg arytmetyczny jeżeli
tworzą ciąg arytmetyczny jeżeli 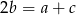 , czyli
, czyli
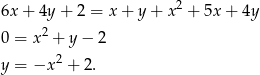
Ciąg jest rosnący, jeżeli
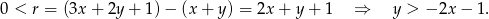
W połączeniu z otrzymaną wcześniej równością daje to nam nierówność
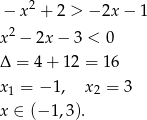
Odpowiedź: