/Szkoła średnia/Ciągi/Arytmetyczny/Trzywyrazowy

Zadanie nr 9877954

Dodaj do ulubionych
Dodaj do rozwiązanych

Sprawdź, czy liczby 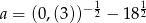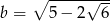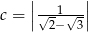− 1 1 a = (0,(3 )) 2 − 182 , ∘ -----√--- b = 5 − 2 6 , ||---1---|| c = |√ 2− √3 | są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.

Rozwiązanie

Zacznijmy od uproszczenia podanych liczb. Najpierw zamieńmy 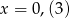x = 0,(3) na ułamek zwykły.

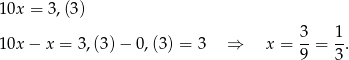
10x = 3,(3) 3- 1- 10x − x = 3,(3)− 0,(3) = 3 ⇒ x = 9 = 3.

Zatem

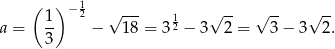
( 1 )− 12 √ --- 1 √ -- √ -- √ -- a = -- − 18 = 3 2 − 3 2 = 3 − 3 2. 3

Ponieważ 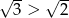√ -- √ -- 3 > 2 mamy

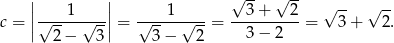
| | √ -- √ -- √ -- √ -- c = ||√---1-√---||= √---1-√---= --3+----2-= 3 + 2. | 2 − 3 | 3− 2 3− 2

Pozostało sprawdzić, czy 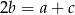2b = a + c . Liczymy

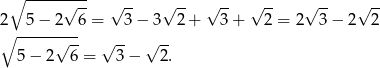
∘ --------- √ -- √ -- √ -- √ -- √ -- √ -- √ -- 2∘ --5−-2---6 = 3 − 3 2 + 3 + 2 = 2 3− 2 2 √ -- √ -- √ -- 5 − 2 6 = 3− 2.

Obie strony są dodatnie, więc możemy podnieść tę równość stronami do kwadratu.

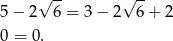
√ -- √ -- 5 − 2 6 = 3− 2 6+ 2 0 = 0 .

Otrzymaliśmy prawdziwą równość, zatem podane liczby istotnie są kolejnymi wyrazami ciągu arytmetycznego.  
Odpowiedź: Tak, są.

Wersja PDF