Zadanie nr 9898641
Jedno z rozwiązań równania 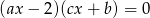 jest równe 6. Ciąg
jest równe 6. Ciąg 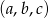 jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
Rozwiązanie
Sposób I
Wiemy, że jedno z wyrażeń 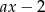 lub
lub 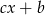 zeruje się dla
zeruje się dla 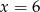 .
.
Jeżeli zeruje się wyrażenie 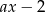 to mamy
to mamy
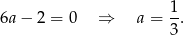
Wtedy 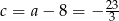 i
i 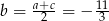 . Pozostało obliczyć drugi pierwiastek
. Pozostało obliczyć drugi pierwiastek
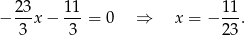
Rozważmy teraz drugą możliwość, gdy 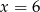 zeruje wyrażenie
zeruje wyrażenie 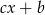 . Mamy wtedy
. Mamy wtedy
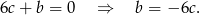
Wiemy ponadto, że
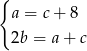
Podstawiamy w ostatniej równości 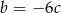 i
i 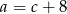 .
.
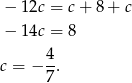
Mamy zatem
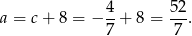
Pozostało wyznaczyć drugi pierwiastek
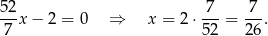
Sposób II
Wiemy, że 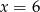 jest pierwiastkiem danego równania zatem
jest pierwiastkiem danego równania zatem
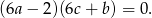
Wiemy ponadto, że 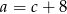 oraz
oraz
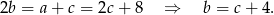
Podstawiamy te wyrażenia do danego równania
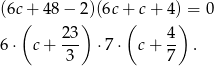
Zatem 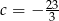 lub
lub 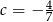 . W pierwszym przypadku pierwiastki równania są równe
. W pierwszym przypadku pierwiastki równania są równe
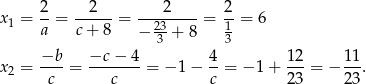
W drugim przypadku są natomiast równe
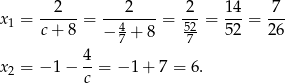
Odpowiedź: 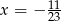 lub
lub 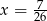 .
.

