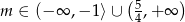Zadanie nr 4410815

Dla jakich wartości parametru 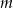równanie 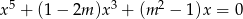5 3 2 x + (1 − 2m )x + (m − 1)x = 0 ma

pięć pierwiastków;
dokładnie 3 pierwiastki;
tylko jeden pierwiastek?

Rozwiązanie

Zapisując równanie w postaci

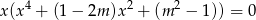
4 2 2 x (x + (1− 2m )x + (m − 1)) = 0

widzimy, że równanie ma zawsze pierwiastek 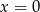x = 0 . Jeżeli podstawimy 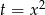t = x 2 to pozostaje do zbadania równanie

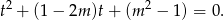
t2 + (1 − 2m )t+ (m 2 − 1) = 0.

Aby równanie miało pięć pierwiastków, powyższe równanie kwadratowe musi mieć dwa rozwiązania dodatnie (żeby równość 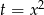dawała cztery różne -y). Sprawdźmy na początek kiedy to równanie ma dwa rozwiązania
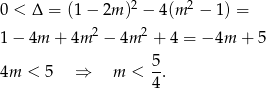
$0 < Δ = (1 − 2m )2 − 4(m 2 − 1) = 2 2 1 − 4m + 4m − 4m + 4 = − 4m + 5 5 4m < 5 ⇒ m < 4.$

Na mocy wzorów Viète’a, rozwiązania będą dodatnie, gdy

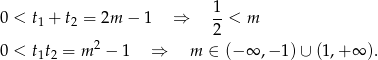
$1 0 < t1 + t2 = 2m − 1 ⇒ --< m 2 2 0 < t1t2 = m − 1 ⇒ m ∈ (− ∞ ,− 1) ∪ (1,+ ∞ ).$

Uwzględniając wszystkie warunki mamy

$( ) m ∈ 1, 5 . 4$

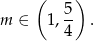
Odpowiedź: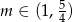
Aby wyjściowe równanie miało dokładnie trzy pierwiastki, równanie kwadratowe musi mieć dokładnie jeden pierwiastek dodatni. Żeby uniknąć kłopotów z zerowym pierwiastkiem, od razu osobno zobaczmy kiedy 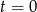jest pierwiastkiem równania kwadratowego. Tak będzie dla 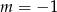lub 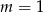. Mamy wtedy odpowiednio równania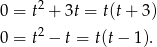
$0 = t2 + 3t = t(t+ 3) 2 0 = t − t = t(t − 1).$

Widać, że będzie OK tylko dla .
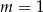Zauważmy jeszcze, że w sytuacji gdy równanie ma dokładnie jedno rozwiązanie, czyli dla 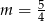, współczynnik przy 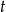jest ujemny, czyli jedyny pierwiastek jest dodatni. Zatem jest OK.
Pozostała nam sytuacja gdy są dwa niezerowe pierwiastki. Aby dokładnie jeden z nich był dodatni, muszą być one różnych znaków, czyli na mocy wzorów Viète’a,

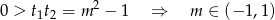
$2 0 > t1t2 = m − 1 ⇒ m ∈ (− 1,1)$

W połączeniu z warunkiem na 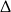-ę i wyżej rozpatrzonymi przypadkami, daje nam to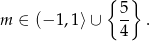

${ } m ∈ (− 1,1⟩ ∪ 5- . 4$

Odpowiedź: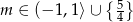
Zastanówmy się ile pierwiastków może mieć wyjściowe równanie? Jest jasne, że może być 1,3 lub 5 pierwiastków. Czy mogą być 2 lub 4? – nie, bo wtedy równanie kwadratowe musiałoby dawać 1 lub 3 pierwiastki, a tak nie może być, bo jeden z nich musiałby być równy 0 (bo 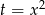), a 0 jest i tak pierwiastkiem wyjściowego równania. Zatem 1 pierwiastek to ostatnia z możliwości i przypadek ten będzie zachodził wtedy, gdy nie zachodzi żaden z poprzednich przypadków, czyli dla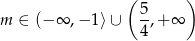
$( 5 ) m ∈ (− ∞ ,− 1⟩∪ --,+ ∞ 4$

Odpowiedź: