Zadanie nr 5455135
Wyznacz wszystkie całkowite wartości parametru 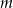 , dla których równanie
, dla których równanie
![3 2 [ 2 2 ] (x + 2x + 2x + 1 ) x − (2m + 1)x + m + m = 0](https://img.zadania.info/zad/5455135/HzadT1x.gif)
ma trzy, parami różne, pierwiastki rzeczywiste, takie że jeden z nich jest średnią arytmetyczną dwóch pozostałych.
Rozwiązanie
Zauważmy, że bardzo łatwo jest znaleźć pierwiastki wielomianu w pierwszym nawiasie.
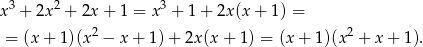
Trójmian w nawiasie nie ma pierwiastków, bo 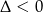 , więc jedynym pierwiastkiem tego wielomianu jest
, więc jedynym pierwiastkiem tego wielomianu jest 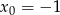 .
.
Zajmijmy się teraz trójmianem w drugim nawiasie.
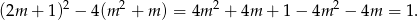
To oznacza, że ten trójmian ma zawsze dwa pierwiastki, które są równe
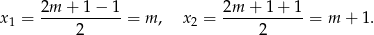
Mamy teraz trzy możliwości.
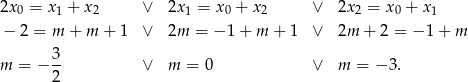
Pierwsza z tych nie jest liczbą całkowitą, więc 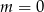 lub
lub 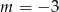 .
.
Odpowiedź: