Zadanie nr 9801521
Dla jakich wartości parametru 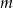 równanie
równanie ![3 2 2 (x + 3x − 4)[(m − 5 )x + (m − 2)x − 1 ] = 0](https://img.zadania.info/zad/9801521/HzadT1x.gif) ma cztery różne pierwiastki?
ma cztery różne pierwiastki?
Rozwiązanie
Na początku znajdźmy pierwiastki równania
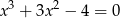
Suma współczynników jest równa 0, więc pierwiastkiem jest 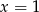 . Dzielimy wielomian przez
. Dzielimy wielomian przez 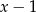 . My zrobimy to grupując wyrazy
. My zrobimy to grupując wyrazy
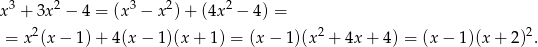
Wielomian ten ma zatem dwa różne pierwiatki 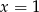 i
i 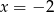 .
.
Pozostało zbadać kiedy równanie
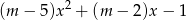
ma dwa pierwiastki, które są różne od 1 i -2. Oczywiście musi być kwadratowe, czyli 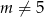 . Ponadto
. Ponadto
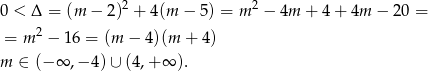
Pozostało sprawdzić kiedy jednym z pierwiastków jest 1 lub -2
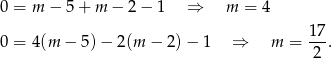
Odpowiedź: